Basic Concepts of One-Dimensional Collisions

Consider two objects, Car A and Car B, moving toward each other on a straight path. Upon collision, forces act upon both vehicles.

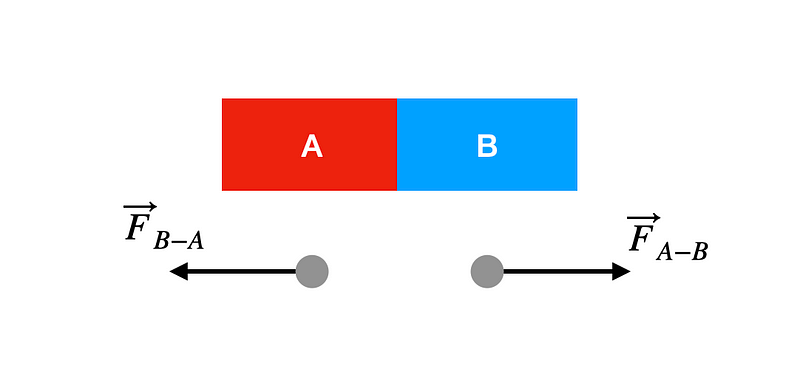
Since forces are interactions between two bodies, the force exerted by Car B on Car A is precisely equal and opposite to the force Car A exerts on Car B. Assuming that this collision force is the sole influence on both vehicles, the net force acting on Car A is denoted as F_B-A. What happens when a net force is applied to an object? It alters its momentum. Recall that momentum (p) is defined as the product of an object's mass (m) and velocity (v).

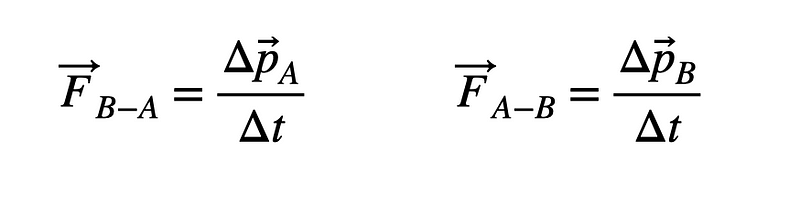
Since both cars experience equal and opposite forces for the same duration (?t), they undergo equal and opposite changes in momentum. We can conclude that the total momentum before the collision is equivalent to the total momentum after it.

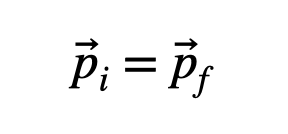
This principle is known as the conservation of momentum. Importantly, I haven't specified the nature of the collision; momentum conservation holds as long as the forces acting on A and B are equal and opposite. However, if one of the vehicles experiences an external force, momentum conservation will not apply.

50–50 Head-On Collision Dynamics

To analyze the damage caused during a collision, we must consider energy. Picture two equal-mass cars colliding head-on, resulting in both vehicles coming to rest. Here’s a relevant animation.

Assuming Car A (the red vehicle) possesses mass m and travels in the positive direction at velocity v, its initial momentum is mv. Conversely, Car B, with the same mass, moves in the negative direction at -v, yielding an initial momentum of -mv. Consequently, the total momentum before the impact is mv - mv = 0, and post-collision, both vehicles are stationary, maintaining a final momentum of zero. Thus, momentum conservation is confirmed.

But how does energy play into this? Both vehicles have kinetic energy prior to the crash. Recall that kinetic energy (KE) is expressed as:

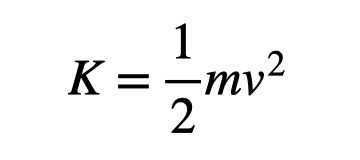
Since kinetic energy is a scalar and always non-negative (as it squares velocity), both Car A and Car B possess (1/2)mv² of kinetic energy before the collision. This sums to a total of mv². However, after the collision, both cars are stationary, resulting in zero total kinetic energy. Where, then, did this energy dissipate?

To visualize a real-world collision scenario, we can observe a physics lab experiment featuring vehicles designed for testing. The right vehicle (Car B) is equipped with an aluminum foil bumper to simulate damage.

While the cars might not come to a complete halt, we can focus on the significant detail: the foil bumper crumples. This deformation signifies a transformation of energy. The kinetic energy wasn't lost; rather, it was converted into other forms, such as the energy needed to deform the foil, plus some thermal and sound energy. This realization is crucial: the alteration in kinetic energy during the collision indicates the extent of damage sustained by the vehicles.

If both cars were to rebound elastically after impact with identical velocities (but in opposite directions) as before, kinetic energy would remain conserved, resulting in no damage or sound.

What if a thin metal wall were positioned at the point of impact? Each car would strike opposite sides simultaneously. The presence of the wall would not significantly alter the outcome. Now, consider a scenario where one car traveling at 50 mph collides with a very sturdy wall. Would the damage be greater, lesser, or the same? This question remains unanswered for now.

100 mph Collision with a Wall

For the next scenario, we will replace Car A with a robust wall while Car B approaches at double the speed. Upon collision, it will halt after hitting the wall.

This setup seems valid, right? Instead of two cars, we now have one car with momentum m(2v). However, let's examine the kinetic energy. Doubling the velocity of one car results in an initial kinetic energy of 2mv² (the square of 2 is 4, so 1/2 multiplied by 4 equals 2). This means the kinetic energy of the single car exceeds that of the two cars traveling at velocity v.

When this faster car collides with a stationary wall, it will stop and lose kinetic energy. All of this kinetic energy translates into "damage" for the car, resulting in four times the damage compared to two vehicles colliding head-on at velocity v.

We can observe this phenomenon in a demonstration using miniature toy cars. In this instance, I simulate a wall by keeping the red car stationary, while I launch the blue car at double the speed using a rubber band pulled back twice as far as before.

The foil bumper compresses significantly more, indicating greater damage to the car.

An important consideration arises regarding momentum. Before the collision, Car B's momentum is -2mv (in the negative direction). However, if the car comes to a stop after impact, the final momentum becomes zero. Hence, momentum is not conserved in this case. We can express this mathematically:

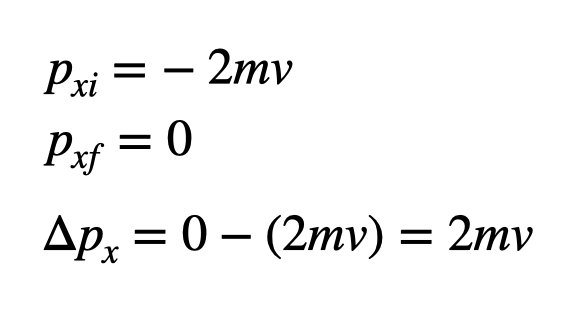
A change in momentum necessitates an external force. In this scenario, we can conceptualize the wall as exerting an external force, leading to a change in momentum and a violation of momentum conservation.

Free-Stationary Target Car Scenario

For our final illustration, the blue car approaches with double the speed while the red car remains stationary (similar to the previous case). However, unlike the last scenario, the red car is free to move post-impact.

In this case, the foil bumper does not compress as severely as in the previous stationary scenario. Why is this so? While the blue car possesses quadruple the kinetic energy compared to the two-cars-colliding scenario, the red car recoils and gains kinetic energy afterward. Remarkably, this collision inflicts the same damage as the 50–50 head-on collision.

Let's analyze the math for this case (assuming the cars stick together post-collision, which doesn't perfectly occur in practice):

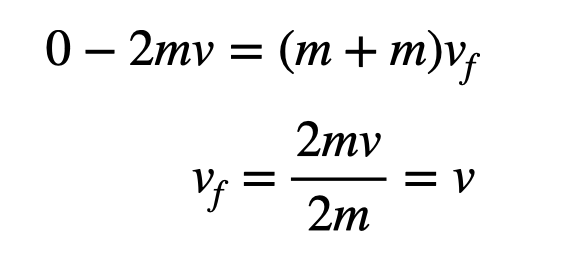
In this instance, the blue car's initial velocity is noted as -2v. Since the total momentum remains constant, both masses will attain a final speed of v (half the initial velocity). Although it may appear unusual, this formulation aligns with the velocity of the two cars during the head-on collision.

Now, let’s consider the change in kinetic energy. The reduction in kinetic energy will equate to the combined damage sustained by both vehicles.

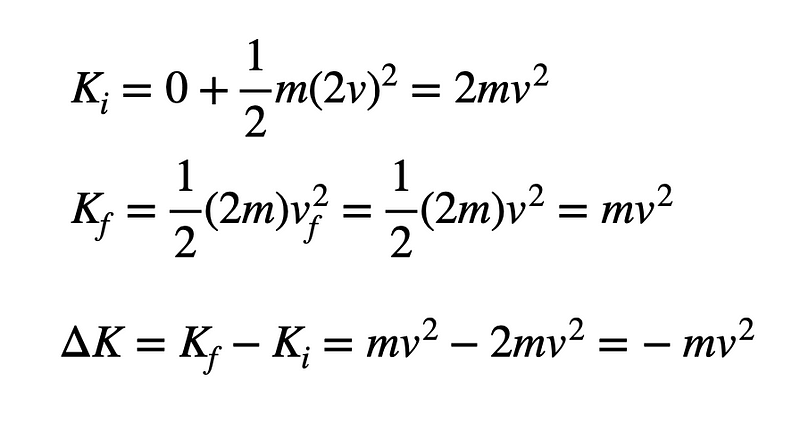
A loss of mv² in kinetic energy implies that each car incurs damage equivalent to 1/2 mv², precisely matching the outcome of the two cars colliding head-on at velocity v.

Exploring Different Reference Frames

Let’s delve into a fascinating concept. In the previous scenarios, I utilized a reference frame stationary in relation to the ground. However, we can adopt a different approach. Imagine the red car is initially stationary while we use a reference frame moving to the left at speed v.

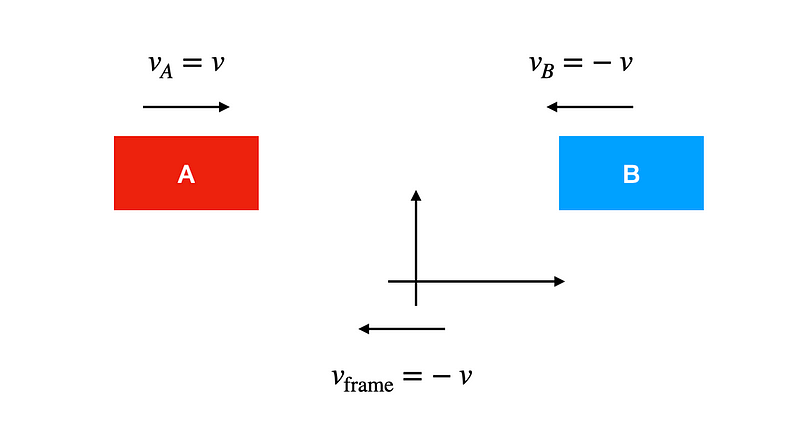
In this moving reference frame, Car A is now perceived as moving to the right at speed v, while Car B travels to the left at speed -v.

The calculations mirror those of the initial case. But wait! In this instance, the total kinetic energy before the collision is mv², whereas if the reference frame is stationary, the total is 2mv². How can these values be equivalent? The total energy is different, but the change in energy remains constant across both scenarios.

This distinction emphasizes that the change in kinetic energy is what truly matters, as it correlates with the damage sustained during collisions.

This insight is significant: it demonstrates that the laws of physics are consistent across various reference frames. The underlying principles remain unchanged, whether we are analyzing a moving spacecraft or a stationary Earth. There is no absolute frame of reference in the universe, which is both intriguing and enlightening.

The first video provides a visual explanation of whether a 50 mph - 50 mph collision is equivalent to a 100 mph collision into a wall.

The second video explores if a 50-50 head-on crash is the same as a 100-0 crash.