Exploring the Visualization of Tensors in Mathematics and Physics
Written on
Chapter 1: Introduction to Tensor Visualization
Before diving into the main subject, I want to share that I've successfully completed the arc on Differential Forms (previously known as the Mathematical Objects arc) by publishing The Generalized Stokes’ Theorem. Be sure to check it out through the link provided earlier if the one below causes issues.
This theorem is pivotal in the field, so I highly recommend looking at it, as it features much of my best artwork.
Section 1.1: The New Arc on Tensors in Classical Mechanics
I'm excited to announce the launch of a new series focused on significant tensors in Classical Mechanics, distinct from Differential Forms. You might be concerned about my workload, but I’ve already drafted half of the articles. The process I follow for writing is as follows:
- Write about a specific topic.
- Realize the need for a deeper explanation.
- Break the article into several sections.
- Repeat until further segmentation is unnecessary.
While I cannot predict my writing trajectory perfectly and may rearrange topics, this method allows me to explore subjects in greater depth, even if it disrupts the series' flow. In fact, the first article in the Tensors in Classical Mechanics series is already well-developed.
Section 1.2: Why Tensors Are Challenging to Illustrate
However, I’ve encountered a dilemma: I struggle with how to visually represent tensors. While some resources exist online and in textbooks, depictions are quite scarce.
If I can't find a better option, I may have to adapt a current depiction from the mentioned video, and I also wish to include representations of covectors.
Subsection 1.2.1: The Importance of Visualizing Tensors
For those who engage with tensors in Physics (as opposed to their usage in data science), visualization isn’t usually necessary for practical application. Consequently, my article is predominantly mathematical, lacking visual components. Yet, a striking featured image is essential to attract readers.
Section 1.3: Addressing Differential Forms
Differential Forms present the simplest tensors to depict, but I have already utilized existing illustrations in previous articles.

What About Specific Tensors?
Many specific tensors could be illustrated, such as stress or strain tensors, which frequently appear in visual examples.
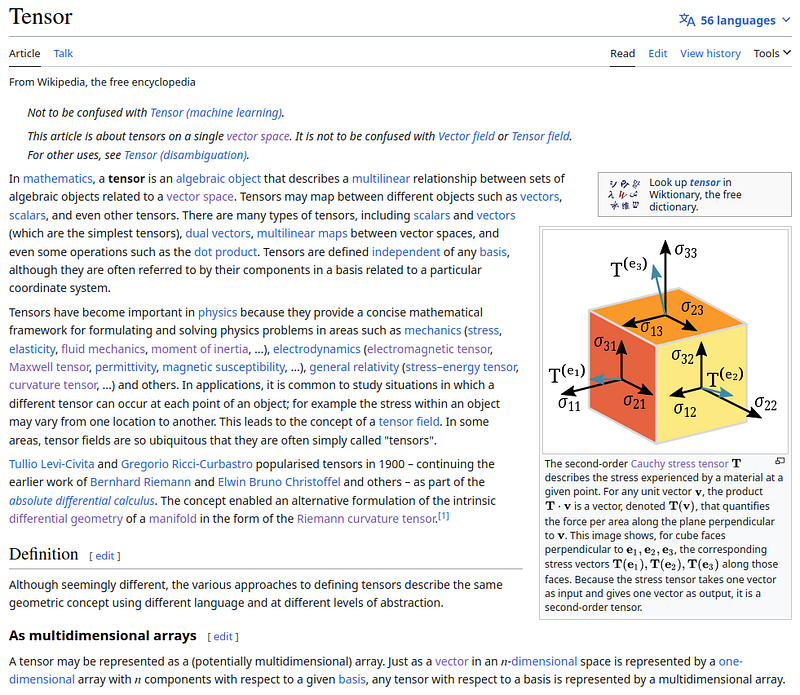
In addition, visual representations like the Riemann curvature tensor exist, but I intend to reserve these for future articles dedicated to those concepts.
Section 1.4: Future Directions in Tensor Research
I aim to create artwork that highlights tensors as transformations—perhaps illustrating a vector on the left, the tensor in the center, and the resulting vector on the right. An amusing remark such as “This is a matrix” could accompany the tensor image.
Subsection 1.4.1: Upcoming Articles in the New Series
The initial plan for the Tensors in Classical Mechanics arc includes:
- An Intro to Tensors
- The Levi-Civita Symbol and Alternating Tensors
- Rigid Body Dynamics and the Inertia Tensor
- The Multipole Expansion
- The Physics of Elasticity
- Maxwell’s Equations and Differential Forms
I have completed the articles on An Intro to Tensors and Maxwell’s Equations and Differential Forms, and I am well on my way with several others.
Section 1.5: Exploring Fluid Mechanics
To delve into Fluid Mechanics, I would need resources focusing on the topic through the lens of tensors or differential forms. A variety of perspectives would be beneficial, ranging from engineering resources that present formulas with practical examples to rigorous mathematical texts devoid of examples. My aim would be to develop content that derives principles from first concepts, beginning with simplified equations like the Euler or Cauchy equations, and discussing their generalizations.
This exploration may follow The Physics of Elasticity or be included in an appendix, depending on the relevance of tensors to Fluid Mechanics. I suspect that with a blend of Quantum Mechanics and statistical mechanics, one could calculate various fluid properties like viscosity.
Chapter 2: Electromagnetism and Relativity
Following this, I plan to tackle the Electromagnetism and Relativity arc, which will likely be subdivided. The current topics include:
- Lagrangian Field Theory
- The Electromagnetic Lagrangian
- Electromagnetic Waves
- Classical Electromagnetism in Materials
- Electromagnetic Optics
- Time Dilation and Length Contraction
- The Lorentz Transformation
I have finished the first two articles, requiring minimal artwork, and made substantial progress on the third. The subsequent articles are yet to be drafted, and I may integrate Maxwell’s Equations and Differential Forms into this section.
Section 2.1: Considering General Relativity
While remaining focused on Quantum Mechanics, I plan to cover up to the topic of black holes. If those articles prove successful, additional content might be included in an appendix.
Section 2.2: Engaging Topics in Finite Fields
I will alternate between publishing articles in the Finite Fields series and the Road to Quantum Mechanics. The upcoming article will focus on eigenvalues and eigenvectors. Upon completing the Finite Fields series, I will delve into the Numerical Methods series more earnestly.
Section 2.3: Community Contributions
If you have suggestions for imagery creation for future articles or valuable resources on upcoming topics, please share. While I’m well-versed in Differential Geometry and have deep knowledge of Electromagnetism and Relativity, I would greatly appreciate assistance for Fluid Mechanics and Solid Mechanics. Any video lectures, textbooks, or even random PDFs of lecture notes would be incredibly helpful.