Laws of Form

Spencer-Brown crafted his mathematical model to enhance the efficient management of train routes. He categorized states into ‘marked’ and ‘unmarked’ by ascribing value to one state over another. For instance, as a train traverses from one area to another, regions transition from ‘unmarked’ to ‘marked’. As intricate routing challenges emerged, Spencer-Brown discovered that re-entry of equations into themselves resulted in paradoxes; thus, ‘marked’ areas had to be reconciled with ‘unmarked’ ones.

Consider the scenario where a train is tasked with picking up and dropping off packages across different regions. The rule for determining a region's value dictates that its current state shifts to its opposite. Initially, every region is ‘Unmarked’.

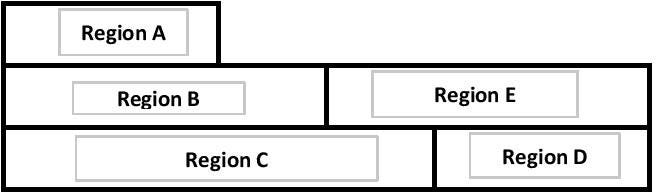
The journey begins in Region A with packages destined for Regions B and C. Upon entering Region B, the region’s state alters from ‘Unmarked’ to ‘Marked’. In Region B, a package is collected for delivery to Region D. As the train progresses through Regions C and D, both these regions transition from ‘Unmarked’ to ‘Marked’. In Region D, another package is gathered for Region B. When the train revisits Region B, the established rule necessitates changing its state back to ‘Unmarked’. In this instance, Region B embodies both ‘Marked’ and ‘Unmarked’ states.

Rather than interpreting this situation as the simultaneous existence of conflicting states, Spencer-Brown proposed viewing the system as oscillating between two opposing states across time. Self-reflexive acts of re-entry introduce a temporal dimension alongside spatial aspects. Over time, both marked and unmarked states can coexist in the same space. In terms of AdS boundaries, entering a boundary, emerging from it, and then re-entering constitutes a ‘self-reflexive act’ of re-entry, adding a time-like dimension to AdS space.

Neuroscientist Francisco Varela expanded on Spencer-Brown’s reasoning by integrating re-entry as a fundamental feature of the initial system. This addition transforms the binary distinction of marked and unmarked (true or false, black or white) into a logic where no middle ground is excluded; the in-between is gray. Varela and Humberto Maturana coined the term ‘autopoiesis’ to illustrate how biological systems self-organize. Autopoietic systems operate independently while remaining functionally closed yet structurally open, embodying a paradoxical foundation.

Mathematically, re-entry can be represented by a fractal equation that is iteratively processed, where the equation's output becomes the input for the same equation. Fractals exist in the complex space bridging ordinary Euclidean dimensions. For instance, a fractal can depict a coastline as a one-dimensional line occupying a two-dimensional area, or mountains as two-dimensional surfaces enveloping a three-dimensional world. A fractal dimension gauges how information becomes more abundant as the measuring device diminishes in size, assessing the quality of relationships between observer and observed. Fractal patterns exhibit self-similarity.

In the context of AdS space, a fractal illustrates how bulk space content manifests at the boundary. An AdS boundary possesses both holographic and fractal qualities. As content repeatedly re-enters boundaries, its complexity escalates, aligning with the quantum principle that states, ‘What can happen, does happen,’ even if numerous re-entries are needed before intricate structures materialize.

Laws of Form and Klein Bottle Topology

When applying Spencer-Brown’s Laws of Form to an AdS space structured like a Klein bottle, a shape transitions between ‘upright’ and ‘upside down’. Completing a rotation within a Klein bottle results in two shapes: one ‘upright’ and the other ‘upside down’. After another rotation, the ‘upright’ shape re-emerges. When these shapes are perceived as holograms on a boundary where time is compressed, the historical sequence of identical ‘upright’ shapes may be encapsulated within a singular shape inside a self-similar form. Mathematically, this process is represented as a fractal or recursive equation, where the outcome of one point in the sequence serves as input for the next output.

An AdS space with a Klein bottle topology introduces a fourth, time-like dimension. As detailed in subsequent articles, Professor Carlo Rovelli has introduced a cosmological theory known as Loop Quantum Gravity (LQG). In his framework, the fabric of space comprises mathematical entities termed spin-foam, resembling soap bubbles that connect in various shapes and sizes to create a network. Another aspect of LQG is that past information is woven into the fabric of space-time. Many concepts in LQG appear to align with the descriptions of space-time presented in these articles.

The five Platonic solids are geometric fractals. Each Platonic solid can seamlessly fit within itself and outside itself, aligning perfectly. This nesting can theoretically continue inward and outward indefinitely. The Platonic solids interconnect as a set in numerous ways, transitioning between forms while preserving self-similarity at all scales.

The fabric of AdS space is composed of shapes, and due to numerous traversals through Klein bottles, the dimensions of shapes at the boundaries of AdS space expand. The magnitude of these shapes can be measured by the count of smaller shapes contained within a larger one; refer to this figure as ‘scale’. Mathematically, the scale of shapes at repetition t, x?, may be equated to the scale of shapes at repetition (t-1) plus a measure of past scale growth. The scale related to how often the same shape reappears must continue to increase since the topology of AdS space, such as a Klein bottle, facilitates continuous repetition. One method to express growth in scale through repetitions is to utilize the same growth observed in the past, i.e., x?-? minus x?-?. The repetition differential is between (t-1) and (t-3) because similar shapes repeat after two cycles. This differential indicates the shortest interval between analogous shapes that will yield continuous growth in scale.

Mathematically:

x? = x?-? + (x?-? — x?-?) is equivalent to:

x? = x?-? + x?-?

This formula representing growth in scale is reminiscent of the Fibonacci sequence, which can be perceived as a time-like dimension. In other words, a time-like dimension emerges in AdS space when its topology resembles that of a Klein bottle. A four-dimensional AdS space includes a boundary where the time-like dimension has been compressed, revealing shapes corresponding to a Fibonacci sequence. This boundary showcases a hologram of infinite space, where a mathematical singularity emerges. The alternation between ‘upright’ and ‘upside down’ shapes, dictated by the topology of AdS space, lays the foundation for the emergence of quantum-like properties within AdS space-time.

As noted in Article 7 - How could mathematics be the foundation for reality, a Platonic solid and its dual can be represented within AdS space by the same mathematical formula in conjunction with a (0, 1) bit of information, where the value is either 0 or 1 depending on which form of the solid is under discussion. This (0, 1) information bit aligns with Spencer-Brown’s ‘marked’ and ‘unmarked’ distinction.

The ratio of two consecutive numbers in the Fibonacci sequence converges to the Golden Ratio (phi). Each of the Platonic solids incorporates the Golden Ratio within their structure. The development of a fourth dimension in AdS space, informed by the time-like Fibonacci sequence, represents a natural progression from an original three-dimensional space consisting of Platonic solids.

Ontological Interpretation of Quantum Mechanics

In 2018, Philippe Grangier and Alexia Auffeves published a paper titled ‘What is quantum in quantum randomness’. Since the outcomes of quantum measurements are influenced by the measurement context, instead of posing the question ‘What value does the variable x have?’, it may be more insightful to ask, ‘What is the value of x when assessed in context y?’ If measurements are taken in varied contexts, i.e., based on differing y values, different values for x may arise without any theoretical contradiction.

Grangier and Auffeves propose an ontological interpretation of quantum mechanics rooted in contextual objectivity. They argue that quantum randomness is a product of contextuality and quantization. In a classical physics framework, epistemic randomness is generally perceived as stemming from incomplete knowledge about a system. However, when physicists assert that complete knowledge of the quantum realm is unattainable, a distinction between classical and quantum randomness becomes essential.

Quantum states do not directly reference the underlying system but instead pertain to the system and context collectively. While systems and contexts exist independently and are ultimately composed of the same elements, only together do they give rise to states that correspond to repeatable phenomena. The notion that systems alone possess states is grounded in a classical worldview.

Grangier and Auffeves argue:

> … in a contextual world, quantizing the amount of exclusive modalities of a system gives rise to some intrinsic unpredictability signaling ontological randomness. … while epistemic randomness is caused by the ignorance of some hidden state, the cause of ontological randomness can be captured by this succinct statement: There are fewer available answers than possible questions. More precisely, the number of possible answers to all conceivable questions exceeds the number of permitted mutually exclusive responses for the system in question. Consequently, some answers are not mutually exclusive and must therefore be related probabilistically — this probability does not signify a lack of information. (p4)

To illustrate what ontological randomness might signify in a human context, consider the following experiment:

1. You are shown this image (the system).

Note: you might perceive one or more of the following interpretations in the image before being informed that it is an image.

Some potential descriptions (contexts) of this system include: - a random arrangement of lines, dots, and spaces; - a sketch of an old woman; and - a sketch of a young girl.

2. Select one context to characterize the image and keep this choice private.
3. When asked a question about the system, you can respond with Yes or No (two exclusive modalities). Essentially, you have two possible responses to each inquiry.
4. All your responses must be coherent, but you do not necessarily need to maintain the same context. For instance, the first question might lead you to perceive a different context. Initially, your context may be random marks on a page. When the first question is “Can you see a picture of a young girl?”, you might find that you can indeed see the young girl. Responding ‘Yes’ shifts your perspective away from random marks. Such a question alters your perceived context of the system. You cannot simultaneously view the image as random marks and as a young girl.
5. Answer all subsequent questions in a manner that preserves consistency with your earlier responses, i.e., provide Yes/No answers that do not contradict prior Yes/No responses.

Before the experiment commences, the administrator is unaware of which context will be perceived. Theoretically, the number of possible answers to potential questions exceeds the number of allowed mutually exclusive answers when responses must remain consistent. At the experiment's outset, the chosen context is deemed an ontologically random outcome, reflecting the participant's free will in selecting their context.

Grangier and Auffeves emphasize that quantum randomness can manifest without the randomness's cause being a lack of information. The randomness inherent in quantum mechanics is intrinsic. Professor John Wheeler, a contemporary of Einstein and Bohr, discussed a game he believed offered insights into quantum mechanics. This game, referred to as ‘Surprise 20 Questions’, entails one person asking questions while different individuals take turns answering. Responses, which must be either Yes or No, must also align with previous answers. The questioner's objective is to guess the object that the last respondent has in mind.

As each participant can conceive their own object without knowing what previous respondents had imagined, no one initially knows what the ultimate object will be. Analogously, prior to a physicist determining how to observe an electron, the electron exists neither as a wave nor a particle. Only after posing a question can the electron be observed, with the selected answer influencing subsequent possible questions.

Ontological Randomness in AdS Space

By merging ontological randomness with Spencer-Brown’s Laws of Form in the context of AdS black holes, the shape of a Platonic solid may represent either the original solid or its dual, depending on how many times that solid has traversed boundaries. In the framework of Wheeler’s Surprise 20 Questions, only two responses are feasible to questions, namely 0 or 1, but the chosen answer could hinge on prior inquiries regarding how many times a solid has crossed a boundary. As hypothesized by Varela, continuous re-entry leads to a logic where both 0 and 1 are attainable, as well as values in between. Since there are more potential questions than answers, the content of AdS space comprises quantum-like bits of information.

The value of the (0, 1) information bit is linked to the historical journey of a Platonic solid. This history implies a ‘before’ and ‘after’ but lacks a definitive arrow of time. Associating information bits with history plays a crucial role in evaluating the concepts discussed in these articles, particularly concerning the influence of gravity.

The presence of quantum-like bits of information in AdS space contributes to explaining how novel phenomena arise within a boundary. The second aspect of this explanation, the Efimov effect, will be addressed in the following article.

The question posed by this article is:

Can the emergence of quantum phenomena be logically explained through mathematics?

A copy of the book ‘Orbiting Stars’ by Michael Dalton contains the initial drafts of all these articles. For more information, please visit https://www.amazon.com.

To view the headings of all articles to be published in this series, click on https://readmedium.com/orbiting-stars-and-origin-of-our-universe-338906930f51.