Chapter 1: Introduction to the Puzzle

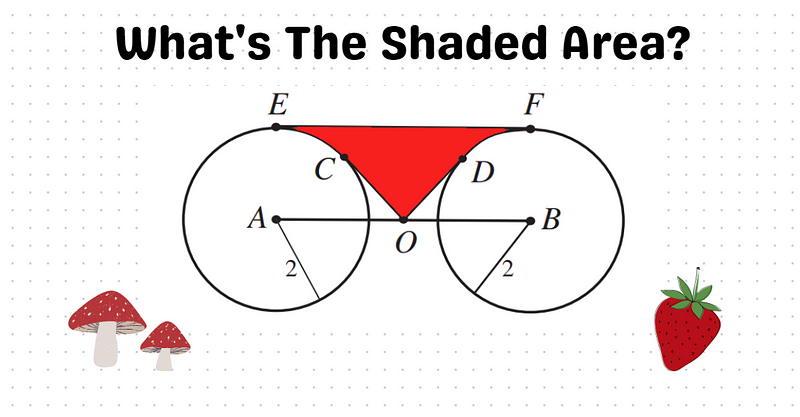
Are you ready to tackle a delightful geometry challenge? This puzzle invites you to examine two circles centered at points A and B, each with a radius of 2. The point O lies at the midpoint of the line segment AB, with the length of OA being 2√2. The segments OC and OD serve as tangents to both circles, while EF represents a common tangent line.

Can you determine the area of the shaded region ECODF? Here’s a tip: a rectangle will play a crucial role in your solution. Take a moment to pause, grab your pen and paper, and give it a shot. Once you’re ready, continue reading for the solution!

Section 1.1: Discovering the Rectangle

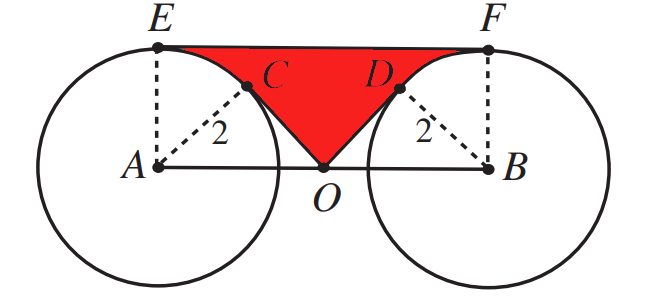
To solve this puzzle, the first step is to visualize and create a rectangle by connecting points E to A and F to B.

The rectangle’s width consists of segments OA and OB, which are equal in length. Thus, the total width is calculated as 2(2√2) = 4√2. The height, corresponding to the radius of the circles, measures 2.

Section 1.2: Calculating Areas

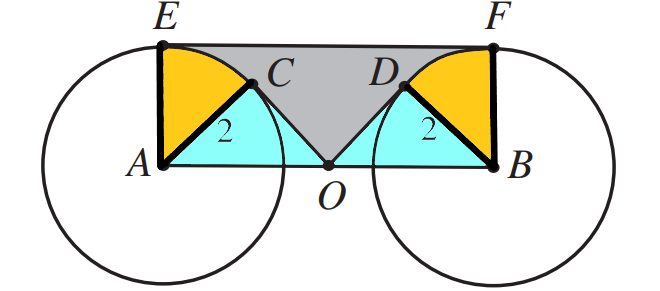
Now, we need to assess the area of the non-shaded regions within the triangle and subtract them from the total area of the triangle. We can identify two non-shaded triangles and two circular sectors.

Identifying the Blue Triangles

The triangles we’re focusing on have OA measuring 2√2, serving as the hypotenuse. One leg of triangle AC is known to be 2. By applying the Pythagorean theorem, we derive OC² + 2² = (2√2)². This results in OC equaling 2√2. Consequently, the two triangles are isosceles, each with an area calculated as:

Area = 1/2 × (2) × (2) = 2

Thus, the total area of the triangles is:

Total area = 2 × 2 = 4

Exploring the Yellow Sectors

As both triangles are isosceles and right-angled, we can conclude that the angles of the sectors are each 45 degrees. Given that the radius of the circles is 2, the area for each sector is:

Area = (45/360) × π × (2²) = π/2

Thus, the combined area of the two sectors is:

Total area = 2 × (π/2) = π

Now that we have the areas of the rectangle and the non-shaded regions, we can compute the area of the shaded region.

Chapter 2: Finding the Shaded Area

In this video titled "Fun Geometry Puzzle," you'll find an engaging walkthrough of the puzzle, explaining the necessary steps to uncover the solution.

The next video, "A Quick Geometry Puzzle," provides a concise and entertaining perspective on solving geometry challenges.

In conclusion, that’s how you arrive at the solution to this captivating problem.

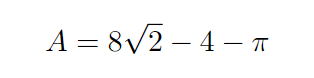
What were your thoughts during this challenge? Share your insights below; I’m keen to hear from you!

Thank you for joining me in exploring this intriguing math puzzle. If you enjoyed it, don't forget to share it with friends who love math challenges.

Thank you for reading! If you found this article helpful, please consider giving it a clap. Your support means a lot!

If you’d like to support my writing journey, consider buying me a coffee. It’s a wonderful way to encourage my efforts. Happy solving!