Exploring the Digit Counting Challenge from Jarník Competition
Written on
Chapter 1: Introduction to the Problem
The digit counting puzzle presented in the Vojtěch Jarník International Mathematical Competition is a captivating challenge. Although lesser-known globally, this undergraduate competition has expanded significantly, now featuring nearly 40 universities from across Europe. In this piece, we invite readers to engage with the problem and share our approach to solving it.
To begin, experimenting with the cif function reveals that the values tend to decrease with each iteration. For instance, cif(99) results in 18, and cif(1274) yields 14. This pattern holds true for any number with two or more digits, which is easy to verify.
Next, let’s express a number ( n ) in a formal way:
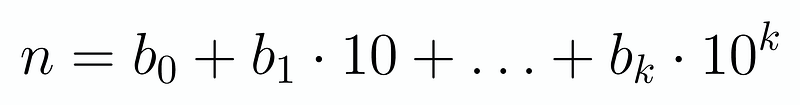
Here, ( b_i ) represents the coefficients of the number. For example, ( 234 ) can be broken down into ( 4 + 3 times 10 + 2 times 100 ). Given that cif(n) is the sum of the digits, we can represent this as follows:
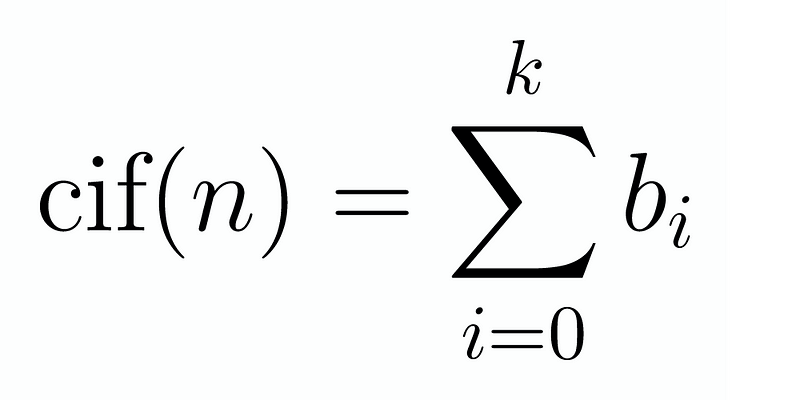
It is natural to consider this sum modulo 9. For those unfamiliar with modular arithmetic, there is an insightful article available for further reading. In this context, each term ( 10^m ) simplifies to ( 1^m ), which is simply 1. Therefore, we arrive at:
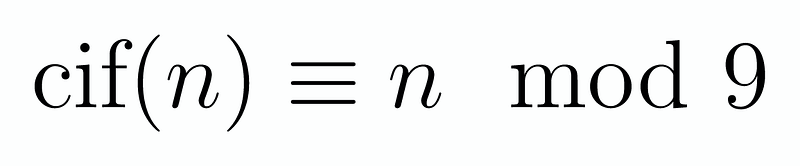
With this understanding, we can now tackle the problem effectively. Observing that cif(n) consistently decreases for numbers with two or more digits suggests that it converges to a single digit. Since cif(n) equals ( n ) for single-digit numbers, we can conclude that convergence occurs. Our task is to find a single-digit number ( k ) such that:
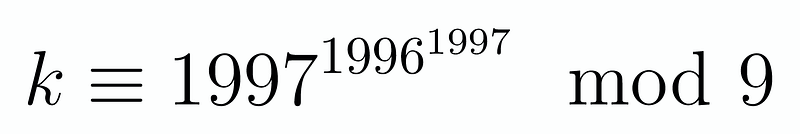
To explore this, we can start by reducing 1997 mod 9. Notably, we can express 1997 as ( 1800 + 180 + 9 + 8 ). Therefore, we have:
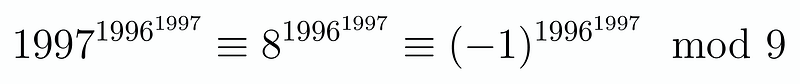
Importantly, ( 1996 ) is always an even number, implying that it must be congruent to 1 mod 9. Hence, we arrive at our final result:
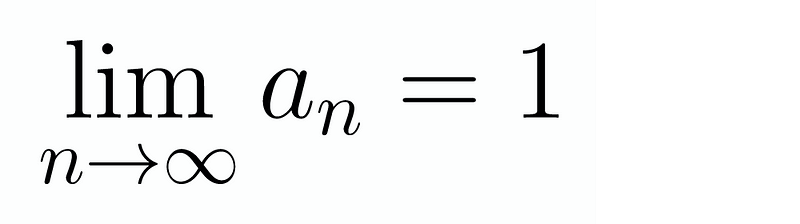
This is indeed a fascinating outcome!