Unraveling the Equation for Reversing Entropy

Our examination of entropy is crucial to addressing the question: "Can we defy the Earth’s inevitable fate?" In previous discussions, we encountered a statistical interpretation of the second law of thermodynamics. This law suggests that the majority of possible states in our universe resemble those of maximum entropy. Given the remarkably low-entropy state post-Big Bang, it follows that most paths through history tend toward rising total entropy. Thus, our universe is on a trajectory toward maximum entropy in the distant future.

Steampunk Clockwork Dreams: The Thermodynamic Revolution of Ludwig Boltzmann

Can we defy the Earth? Part 4

The statistical theory is intriguing yet not the most straightforward for addressing our core inquiry: If we aim to reverse a system's entropy, how much work is required? This understanding is essential for tackling our main question: "Can we defy the Earth?"

In our last discussion, we examined Carnot's principles regarding entropy through the lens of a reversible heat engine, which demonstrates that heat can be transferred against its natural flow, albeit at a cost of work.

What is Temperature, Really?

Can We Defy the Earth? Part 5

Carnot’s analysis provides a concise response to how much work is necessary to reduce a system's entropy by a specific amount. This always corresponds to a larger increase in entropy elsewhere.

This inquiry is pertinent for engineers designing refrigerators, quantum systems, or even when resetting a computer's memory from a randomized state. The theoretical energy required to bring back the dead could also be framed here! However, while it highlights the minimum energy needed, it does not offer a practical method for accomplishing this.

To transfer a quantity of heat ( Delta Q ) from a cooler reservoir at temperature ( T_c ) to a warmer one at temperature ( T_h ), we know from Carnot’s perspective that the entropy of the cold reservoir decreases by an amount ( Delta S = -Delta Q/T_c ). Balancing that entropy when releasing heat into the hot reservoir requires a greater quantity of heat ( Delta Q ) so that the net change in entropy ( (Delta Q/T_h) - (Delta Q/T_c) geq 0 ). This additional heat must come from work, resulting in the equation:

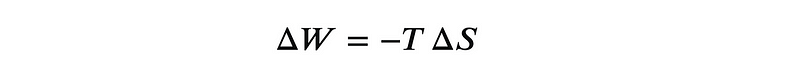
This equation applies to small changes in entropy and forms the basis of our understanding of how to reduce the entropy of a system. This is also the theoretical framework for the energy required to "bring the dead back to life."

A Thought-Provoking Inquiry

It’s important to emphasize that we are discussing averages over extended periods and large populations. The entropy of a system naturally exhibits tiny fluctuations, as explored through fluctuation dynamics. At thermodynamic equilibrium, entropy is equally likely to rise or fall, with systems randomly oscillating around maximum entropy. However, when a system is out of equilibrium, the chances of experiencing a downward fluctuation in entropy become negligible compared to upward fluctuations.

We will also examine the concepts illustrated by Maxwell's Demon and Szilard's Engine to deepen our understanding of these principles.

Engaging with the Enthalpy Dilemma

To grasp why not all energy released in a chemical reaction can be harnessed, consider the amount of energy required to heat a substance to a certain temperature. Different substances have varying heat capacities, affecting how much energy can be converted to work.

A chemical reaction alters the structures and symmetries of its molecules, impacting how energy is stored through molecular movement, including translational, vibrational, and rotational energy. If a reaction results in product molecules that can vibrate in fewer ways than the reactants, the products will have lower entropy.

Let's entertain a hypothetical scenario where we could fully access all internal energy released during a reaction. To make this feasible, we must consider the changes in the surrounding environment. While this might seem impractical for repeated applications, it provides insight into the limits of energy recovery.

Hydrogen: A Case Study in Energy Release

Hydrogen combustion is an exemplary reaction that liberates vast amounts of energy, making it a prime candidate for propulsion applications, such as sending astronauts to the Moon.

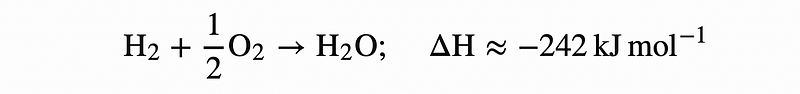
Discussions around hydrogen often highlight its potential for energy storage and transportation, albeit with significant safety considerations due to its explosive nature.

Thermodynamic Implications of Energy Release

When a reaction’s products possess lower internal energy than the reactants, it indicates that energy has been released into the environment. For exothermic reactions, the enthalpy change will be negative, signifying energy release.

Throughout this article, we’ve primarily used ( H ) for enthalpy while maintaining ( S ) for entropy, a convention necessary for clarity despite their underlying connection in thermodynamics.

As we examine hydrogen combustion and its implications, it becomes evident that the energy released corresponds to an increase in entropy in the surrounding environment:

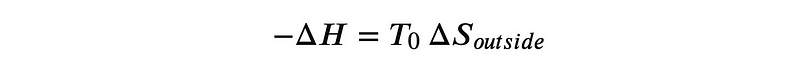
Therefore, the Gibbs energy change is crucial for understanding the spontaneity of reactions. A reaction with a positive Gibbs energy change cannot occur spontaneously, while one with a negative change can, though high activation energy can still hinder spontaneity.

The Fascination of Endothermic Reactions

While many are captivated by exothermic reactions, endothermic processes, such as those seen in ice packs, reveal a different kind of magic. An endothermic reaction absorbs energy from the environment, showcasing the complex interplay between energy transfer and entropy.

By utilizing the principles we've discussed, we can now appreciate how these reactions draw energy from their surroundings, leading to intriguing applications in thermodynamics.

Explore the philosophical depths of thermodynamics in this uplifting video, examining how we grapple with the second law of thermodynamics.

In this video, we investigate the irreversible nature of entropy increase, particularly through the lens of free expansion, enhancing our understanding of thermodynamic principles.