Understanding Anomalies in Elliptical Orbits with Python Visuals
Written on
Visualizing how anomalies in elliptical orbits interact provides insights into the dynamics of celestial bodies. By examining the relationships among the true, eccentric, and mean anomalies, we can gain a clearer understanding of how objects navigate their orbits.
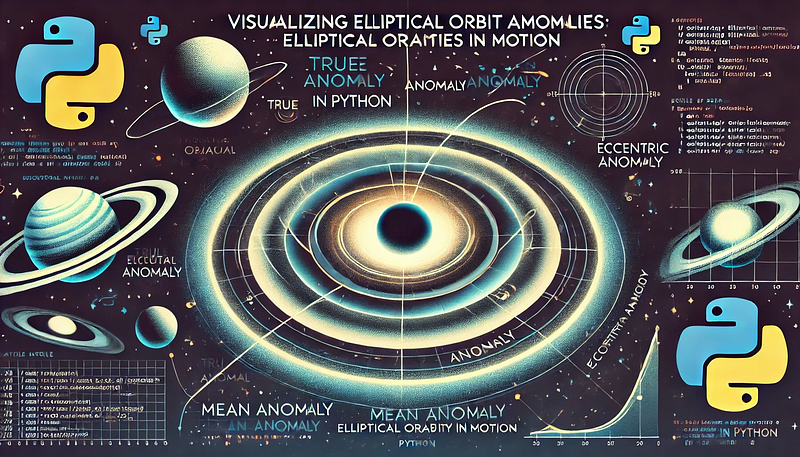
This comprehension is vital for accurately predicting positions, planning space missions, and exploring celestial mechanics. Visual representations simplify complex ideas, making them more approachable and facilitating learning in fields like astronomy and space exploration.
The following figure demonstrates how different anomalies relate within an elliptical orbit, emphasizing its geometric interpretation. Here’s a brief overview of key components:
- Ellipse (orbit): The blue curve depicts the elliptical trajectory of the orbiting body (P).
- Circle: The red curve represents a reference circle sharing the same radius as the ellipse’s semi-major axis, aiding in defining the mean anomaly.
- Primary Focus (c): The point marked ‘c’ indicates one of the foci of the ellipse, typically where the primary body (like the sun) resides.
Equations 1–3 outline the features of an elliptical orbit. The corresponding Python code, along with detailed documentation, clarifies the functions, their parameters, and their applications.
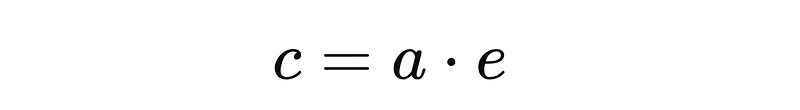
- Periapsis & Apoapsis: Periapsis is the closest point to the primary focus in the orbit, while apoapsis denotes the point where the orbiting body is furthest away. These properties are essential for determining the geometry of an elliptical orbit, including eccentricity and the radii of periapsis and apoapsis.
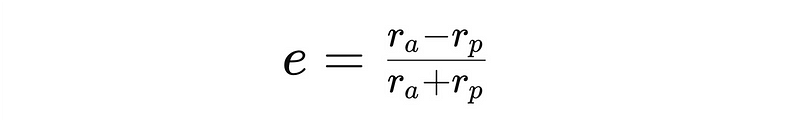
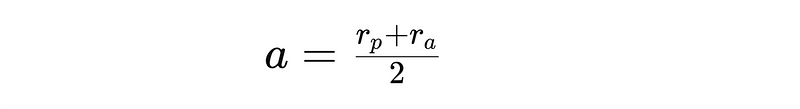
- Orbiting Body (P): The blue dot labeled ‘P’ indicates the current position of the orbiting body along the ellipse.
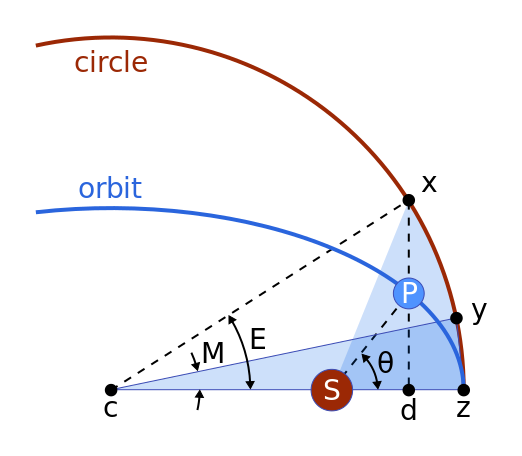
This visualization effectively showcases the geometric relationships among these anomalies, which are crucial for grasping orbital mechanics and determining the position of an orbiting body at any moment.
- True Anomaly (?): This angle measures the true anomaly, representing the angle between the direction of periapsis and the orbiting body's current position at the primary focus (c).
Equation 4, known as the orbit equation, defines the trajectory of body m? around body m?, relative to ??. The variables ?, ?, and ? remain constant.
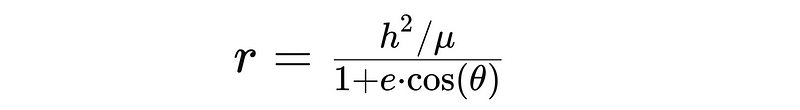
- Eccentric Anomaly (E): This refers to the angle in the auxiliary circle that corresponds to the projection of the orbiting body’s position onto the circle.
The simulation in Figure 3 aims to clarify the concept of Eccentric Anomaly.
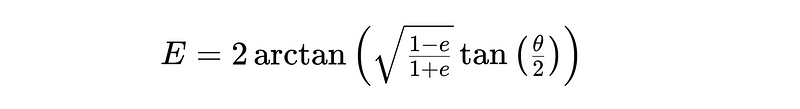
- Mean Anomaly (M): The mean anomaly relates to the area covered by the orbiting body. It is the fraction of the orbital period that has passed since the last periapsis, multiplied by 360° (or 2? radians).
If the Mean Anomaly seems abstract, refer to the simulation in Figure 3 for a more concrete example.
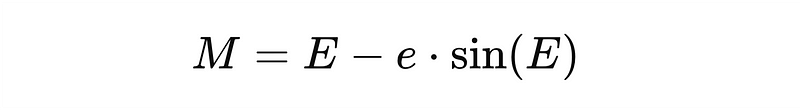
Algorithm
The script computes parameters and positions relevant to an elliptical orbit, organizing this information into a Python pandas DataFrame. The following steps outline the script's functioning, emphasizing that only basic numerical operations are needed.
Orbit Configuration
- Establish constants such as Earth's radius R?, gravitational parameter ?, periapsis radius r?, and apoapsis radius r?.
- Set the true anomaly at periapsis to zero.
Orbital Parameters
- Eccentricity e: Calculate using calc_eccentricity().
- Angular Momentum h: Calculate using calc_angular_momentum().
- Orbital Period T: Calculate using calc_period_from_momentum().
True Anomaly Array:
- Create an array of true anomaly values ? from 0 to 360 degrees, converting to radians with deg2rad().
Anomalies and Times:
- Eccentric Anomaly E: Calculate using calc_eccentric_anomaly().
- Mean Anomaly M?: Calculate using calc_mean_anomaly().
- Time Since Periapsis t?: Calculate using calc_time_since_periapsis().
Elliptical Geometry:
- Semi-Major Axis a: Calculate using calc_semi_major_axis().
- Foci Position c: Calculate using calc_foci_position().
- Semi-Minor Axis b: Calculate using calc_semi_minor_axis().
Orbit Positions:
- Orbit Position r: Calculate using orbit_position().
Cartesian Coordinates
- Calculate the Cartesian coordinates r? and r? for the orbit positions.
- Compute auxiliary circle coordinates.
- Determine Cartesian coordinates for eccentric anomaly and mean anomaly.
Create Pandas DataFrame
Organize all computed values into a pandas DataFrame for efficient storage and easy access.
Simulation
Figure 2 illustrates the visualization of elliptical orbit anomalies.
Explanation of Relationships
- True Anomaly (?): This angle directly measures the orbiting body's position along the ellipse.
- Eccentric Anomaly (E): This angular parameter relates the orbiting body’s position on the ellipse to a circular reference orbit. Dropping a perpendicular from point ‘P’ on the ellipse to the major axis reveals the corresponding angle in the reference circle, which is the eccentric anomaly.
- Mean Anomaly (M): This measures the area swept out by the radius vector from the center of the ellipse to the orbiting body. Unlike the true anomaly, which fluctuates due to the elliptical shape, the mean anomaly offers a consistent measure of time throughout the orbit.
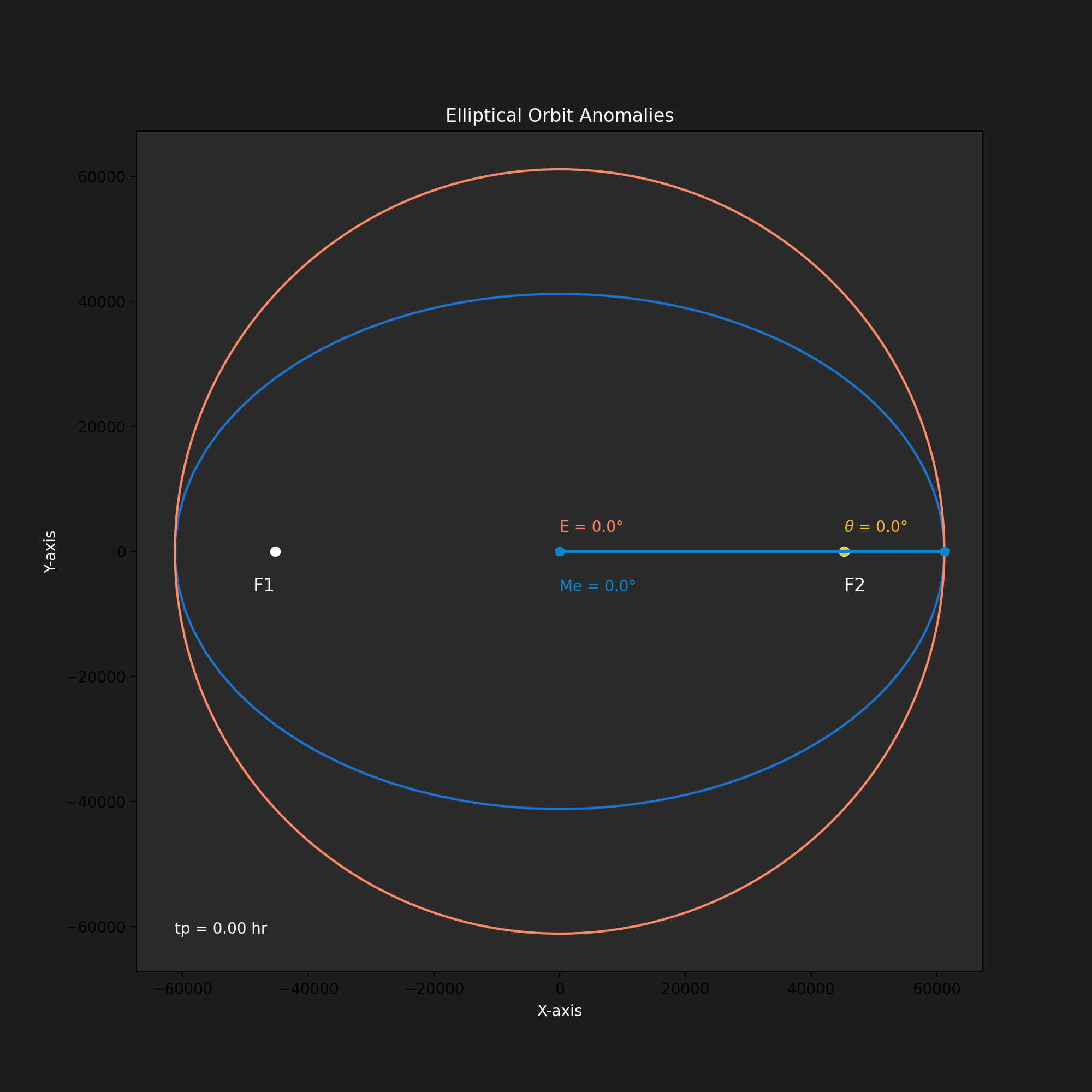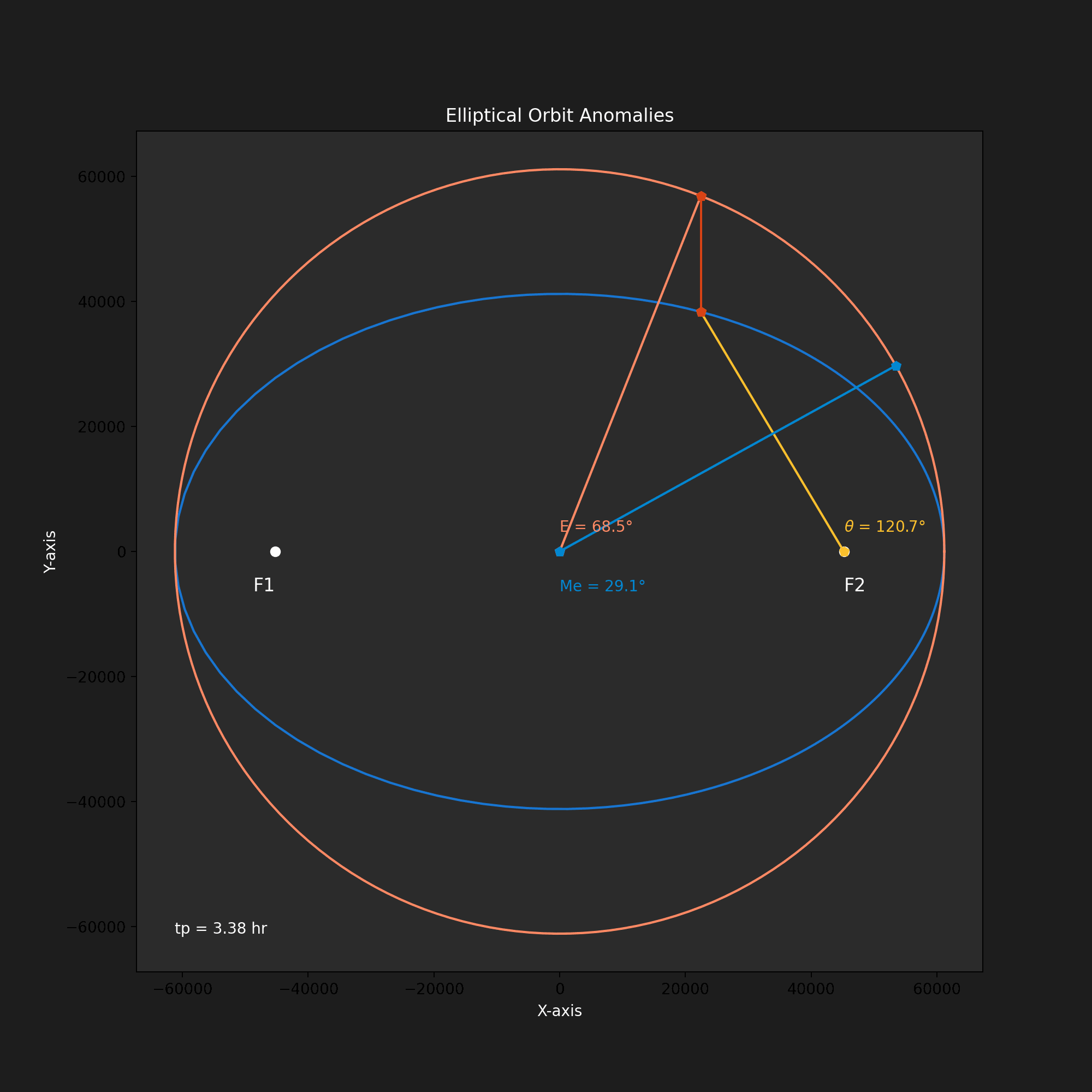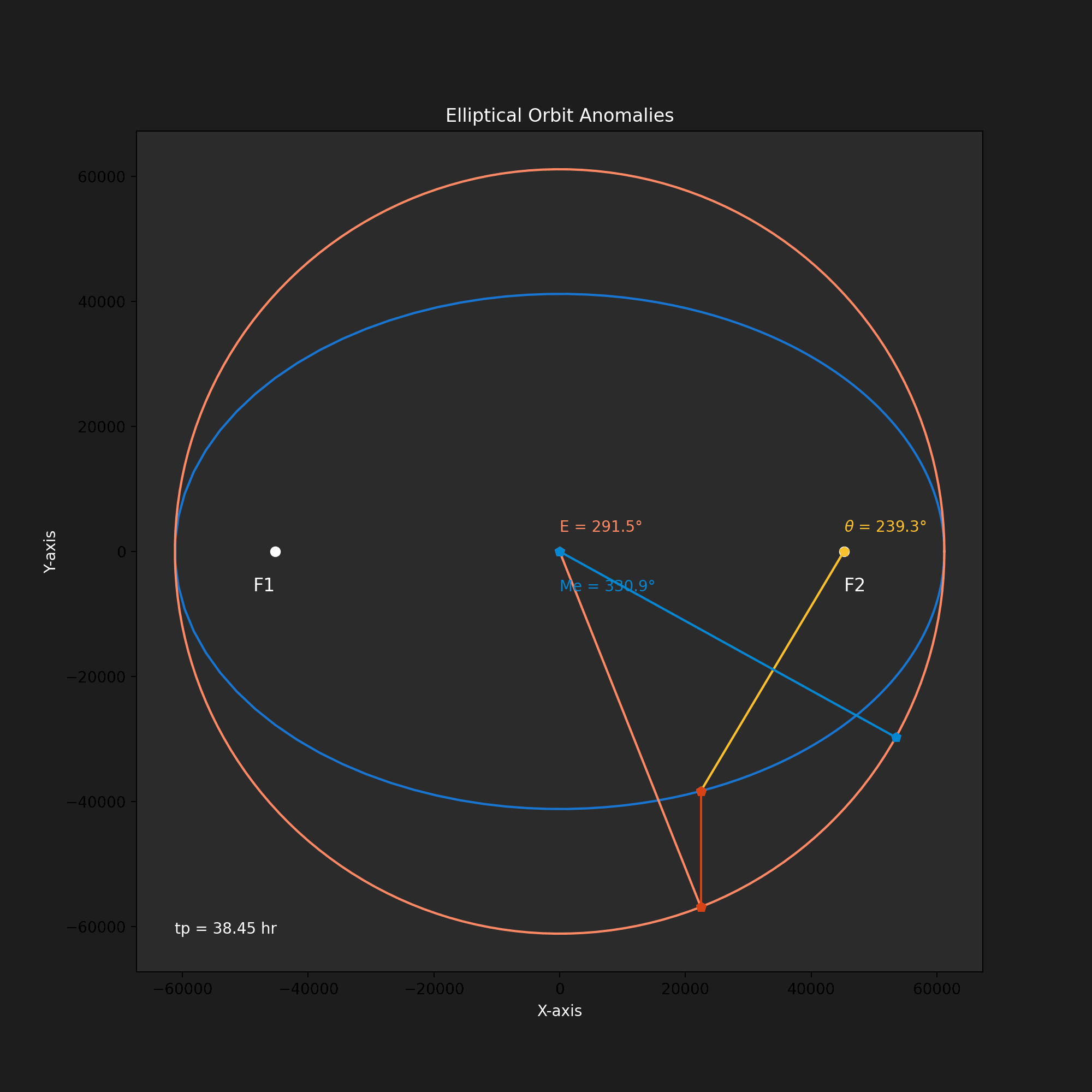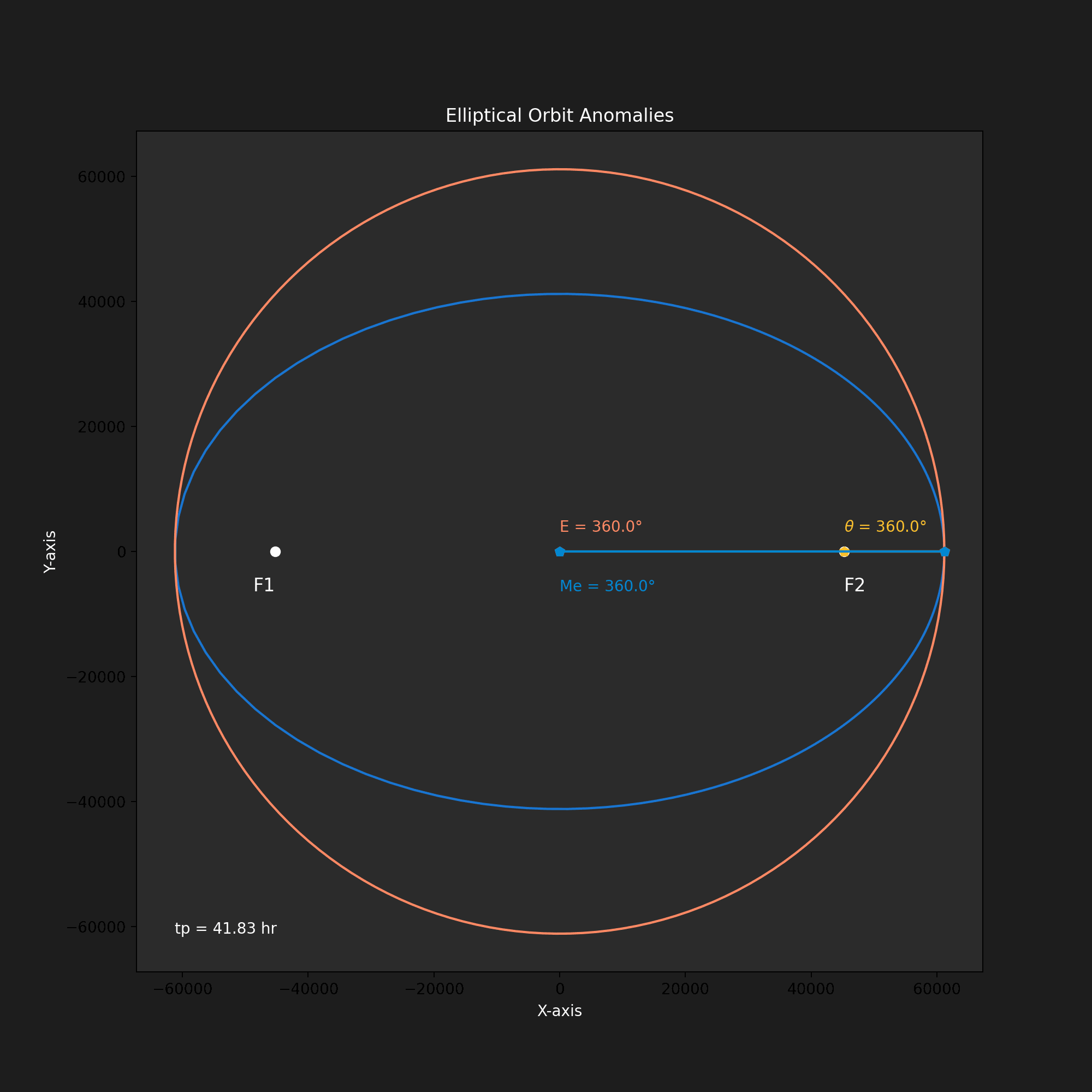
A notable aspect of the animation is that the orbit accelerates near apoapsis and decelerates near periapsis. The time since periapsis t? is noted in the figure.
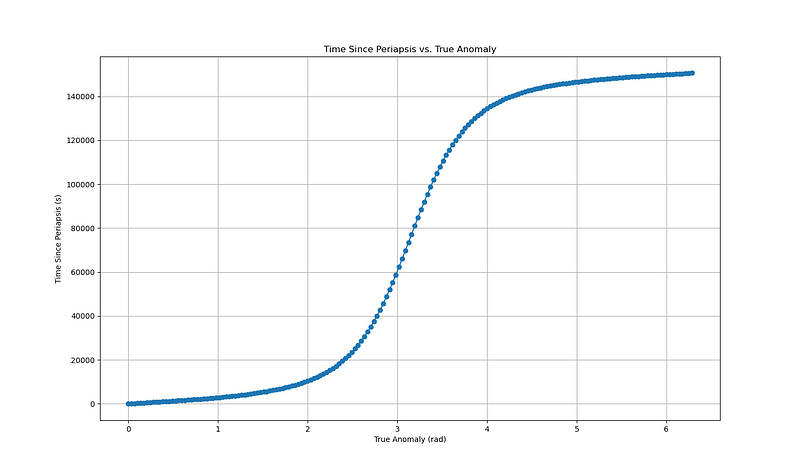
Figure 3 presents a plot of the true anomaly (b) against time since periapsis (t?). Key insights include:
Rapid Increase at Low Anomaly:
- At lower true anomaly values (near 0 rad), t? grows slowly, indicating that the orbiting body moves swiftly in this orbit segment due to stronger gravitational forces at periapsis.
Gradual Increase Near Anomaly ?:
- As the true anomaly nears ? radians (180 degrees), the time since periapsis increases gradually, corresponding to the body’s movement through apoapsis, where gravitational influence is weaker, resulting in a slower orbital speed.
Symmetry of the Orbit:
The graph demonstrates symmetry around ? radians (180 degrees), reflecting the elliptical nature of the orbit, where the time taken to traverse from periapsis to apoapsis mirrors the time taken to return.
Conclusion
This article illustrated how to visualize the anomalies associated with elliptical orbits. The entire approach involves straightforward numerical calculations based on foundational orbital mechanics equations. Each function executes basic arithmetic and trigonometric operations to derive necessary parameters. Specifically, Python visualization serves as a valuable tool for engineering and mathematics students, as it translates abstract concepts into visual formats that enhance understanding.
If you found this exploration of orbital mechanics engaging, consider reading about the Two-Body Problem in Python. This intriguing subject examines the gravitational interactions between two bodies and their mutual influence on each other's motion, offering deeper insights into the principles of celestial movements.
We invite you to check out our additional articles of interest:
The Two-Body Problem in Python
Visualizing the motion of two bodies due to their mutual gravitational attraction.
levelup.gitconnected.com
Similarly, if you’re looking to enhance your machine-learning skills, explore the Semantic Segmentation of Aerial Imagery in Python.
Semantic Segmentation of Aerial Imagery using U-Net in Python
Semantic segmentation of MBRSC aerial imagery of Dubai using a TensorFlow U-Net model in Python.
towardsdatascience.com
We appreciate your feedback and inquiries. Please comment with any questions or topics you’d like us to cover. Your engagement helps us enhance our content to meet your interests and educational needs.
Appendix
The appendix includes additional equations and their corresponding Python implementations necessary for constructing the pandas DataFrame referenced for the Matplotlib animation. This supplementary material provides the essential details to apply the concepts discussed and complete the visualization.
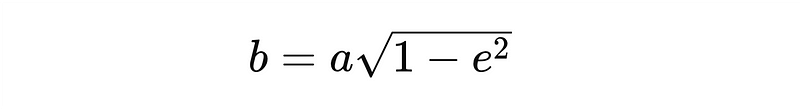
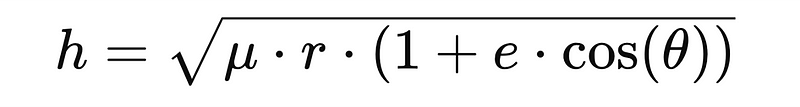
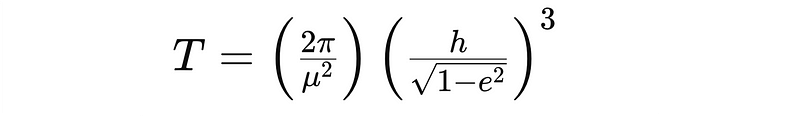
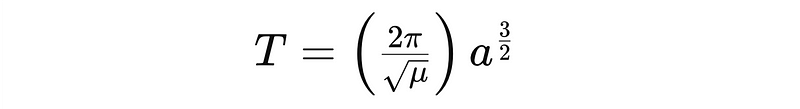
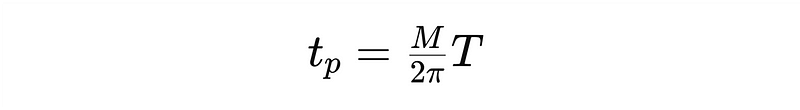
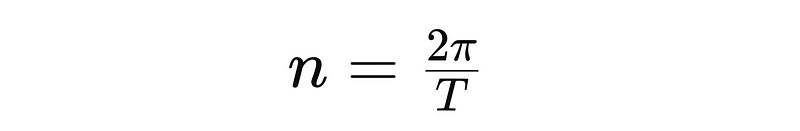
Find all Python code necessary for replicating the simulation below.