First Impressions

I anticipate that this module will primarily cover foundational concepts behind quantum computing, distinguishing it from classical computing. This foundation is essential for understanding more advanced material in subsequent modules. I am particularly keen on exploring Q# and its related case studies.

Module Overview

Classical computers operate by manipulating binary data, known as bits, to address problems and perform computations. In contrast, quantum computers utilize quantum bits, or qubits. Engineers develop programs that engage these qubits indirectly through the principles of quantum interference.

The enhanced capabilities of quantum computers stem from their ability to exist in a superposition of states.

For a quantum computer to be considered effective, it should adhere to the Di Vincenzo criteria, which stipulate that it must be:

1. Scalable: Capable of accommodating numerous qubits.
2. Initializable: Able to reset qubits to a predetermined state.
3. Resilient: Maintains a superposition of states over a relatively extended duration, resisting external disturbances.
4. Universal: Can execute a finite set of operations that form a basis for all other operations, akin to a Turing-complete programming language.
5. Reliable: Capable of measuring qubits with precision.

Microsoft Azure offers a suite of tools for interacting with actual quantum computers globally, including Q#, a high-level quantum programming language. Q# abstracts some complexities associated with quantum dynamics, enabling developers to focus on programming.

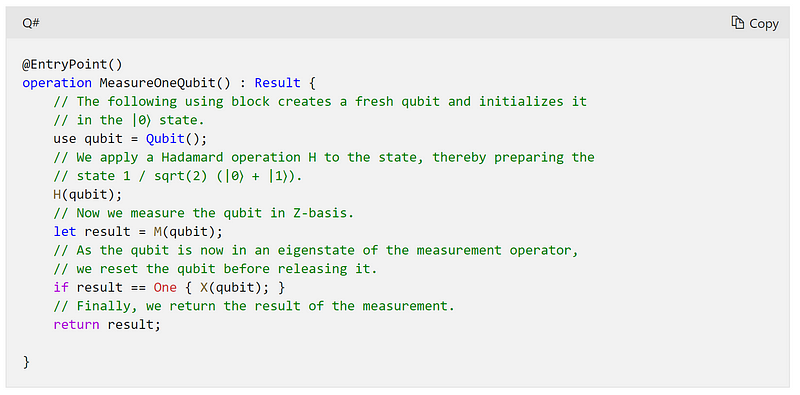
Here is an example of a program crafted in Q#.

Microsoft promotes Azure Quantum and Q# as premier solutions for developing quantum applications. However, it is essential to recognize that quantum computing is not a panacea for every computational issue. Even with the ideal quantum computers, which are still a long way off, some problem classes remain too intricate to resolve in polynomial time using quantum algorithms.

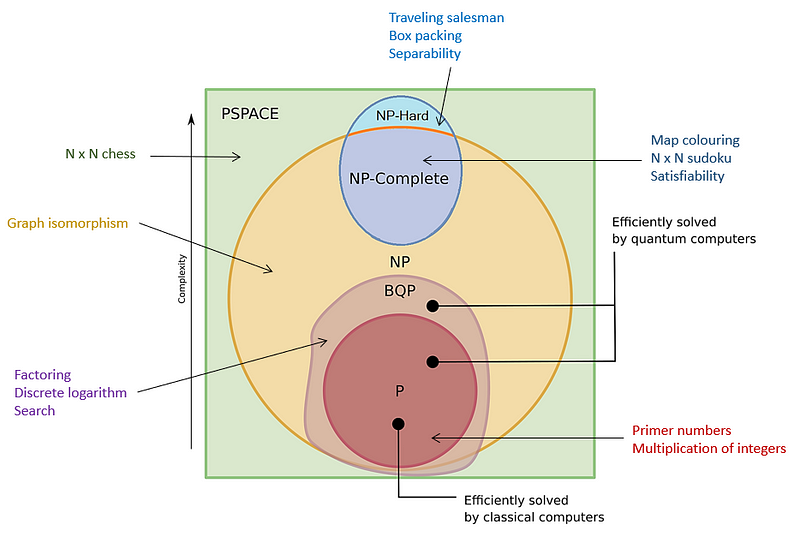
BQP stands for bounded-error quantum polynomials, which are problems solvable in polynomial time via quantum computing.

As one insightful quote goes, "Quantum mechanics is the underlying ‘operating system’ of our universe."

Final Thoughts

I feel quite optimistic after finishing the first module today. Although there were no hands-on activities, and I have no code to showcase, I look forward to sharing more insights in my upcoming article.