Mastering the Art of Generating Numbers Using Four 4s
Written on
The Four 4s Puzzle Explained
The challenge of generating numbers using four 4s can be both fascinating and complex!
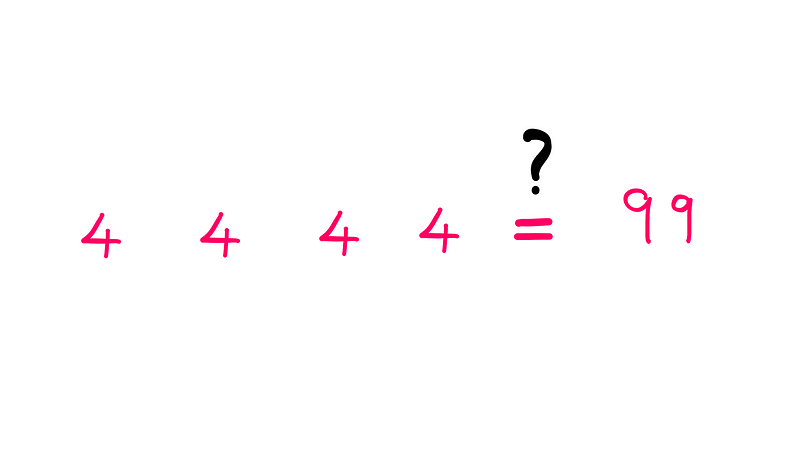
A popular adage states: "Those who master the four 4s need not fear the toughest mathematical challenges!" While I just coined this phrase to justify my exploration of this captivating math puzzle, it does highlight its importance.
This isn’t just any math puzzle; it’s known as the "four 4s puzzle." The premise is straightforward: you have four instances of the number 4 and can use various mathematical operations to combine them in a way that yields any non-negative integer. You can apply any valid mathematical operators to achieve this goal.
To begin, we will focus on the first ten integers, from zero to nine, employing basic operations: addition (+), subtraction (-), multiplication (*), and division (/).
Following that, I will demonstrate how to generate larger integers, which require more advanced mathematical techniques. Ultimately, I will present a general method applicable to any positive integer.
The Four 4s Puzzle — Generating the First Ten Integers
Generating the first ten integers is relatively simple. Below, I’ve worked out the first integer (zero) as an example. You can attempt to find the solutions for the remaining integers (1–9) on your own. For these integers, the fundamental operations and parentheses are all you need.
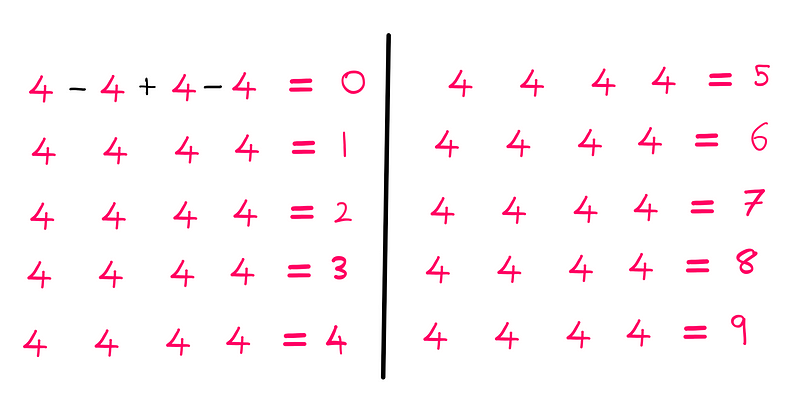
It's important to note that there are multiple solutions to this puzzle. Your approach might differ from mine, and that’s perfectly acceptable!
Spoiler Alert: I will be revealing solutions for the integers from 1 to 10 shortly. If you want to solve them independently, now would be a good time to pause and return later to compare your findings.
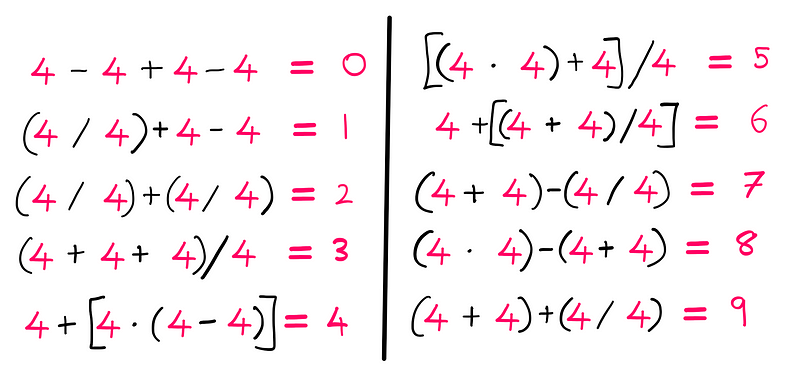
The Four 4s Puzzle — Tackling Larger Integers
As we venture beyond the initial integers, basic operations alone will not suffice to generate larger numbers. Here’s a list of additional operators commonly utilized:

Consider the question posed in the title image: What combination of four 4s results in 99?
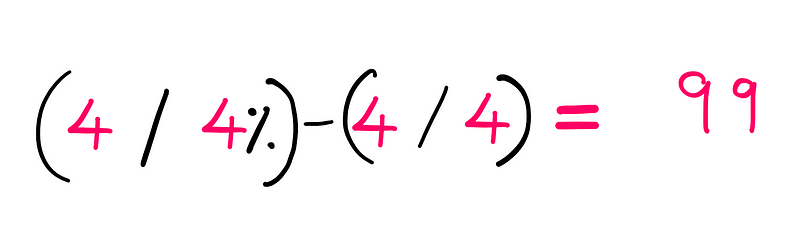
Additionally, mathematicians have explored a variety of other operators to tackle this puzzle. But why not aim for a more comprehensive solution? That’s where we’re headed.
The Four 4s Puzzle — A General Solution
This puzzle has a rich history, dating back to the late 19th century. In the early 1900s, physicist Paul Dirac became intrigued by it and discovered a general solution that accommodates all positive integers. He achieved this using only logarithms and square roots.
To appreciate his ingenious method, we first need to understand two fundamental concepts.
The first is the application of logarithms based on 4. Although we don’t frequently use logarithms in base 4, they are essential for our exploration.
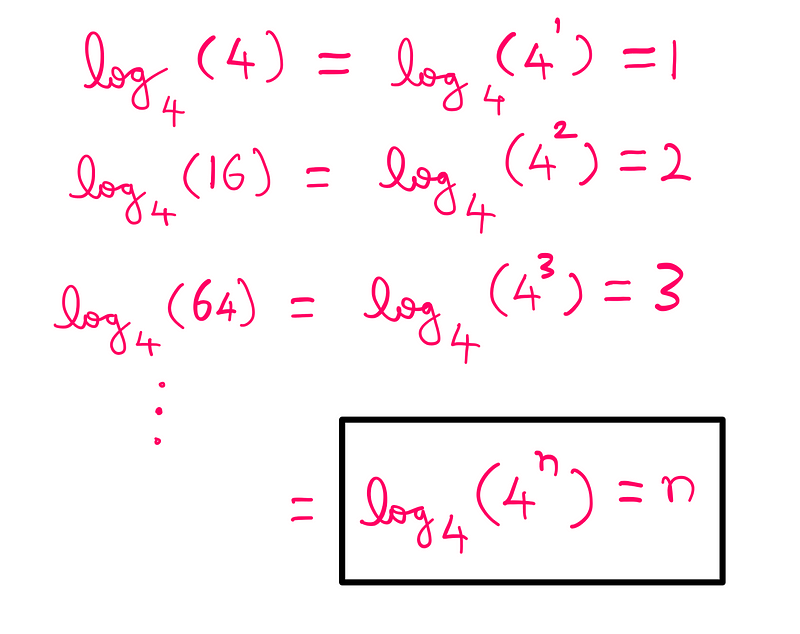
The second concept involves extending our understanding to logarithms with a base of ½.
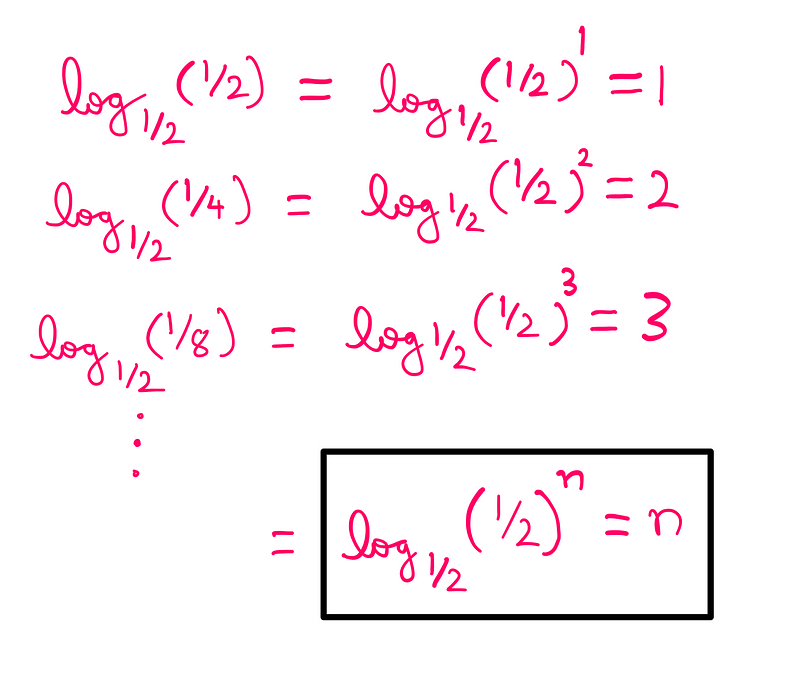
Finally, we express ½ as ?4/4 (which equals 2/4). Now we have all the components necessary to grasp Dirac’s general solution:
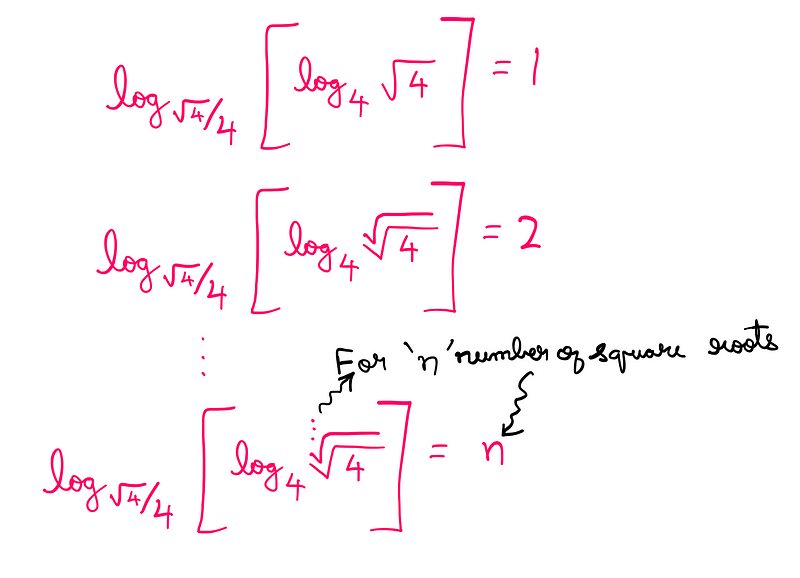
In this expression, four 4s are present, and the number of square roots inside the parentheses dictates the value of n. To generate any arbitrary integer, we simply need to include the corresponding number of square roots.
Concluding Thoughts
Initially, this puzzle seemed simple, but as I explored larger integers, I began to appreciate the complexity it entails. It’s no surprise that brilliant minds like Dirac engaged with this challenge. If you’ve discovered interesting methods for solving this puzzle, please share them in the comments! I hope you enjoyed this exploration as much as I did.
References: Colin Foster and Alex Bellos.
If you’re interested in supporting my work as an author, consider following, subscribing, or showing appreciation. Further reading that may pique your interest includes: How to Mentally Calculate Cube Roots as 2-Digit Integers? and How to Truly Solve the Three 3s Problem?
In this video, explore how to make the numbers 1-20 using only four 4s, demonstrating various mathematical operations.
Check out this engaging Numberphile video that delves deeper into the Four 4s puzzle, showcasing creative approaches to generating numbers.