Exploring Twin Primes: A Mathematical Journey
Written on
Chapter 1: The Legacy of Riemann
In 1859, Bernhard Riemann released a groundbreaking paper in analytic number theory that significantly influenced the understanding of prime number distribution. The paper, titled "Über die Anzahl der Primzahlen unter einer gegebenen Größe," translates to "On the Number of Primes Less than a Given Magnitude." Riemann explored the zeta function—now famously known as the Riemann zeta function—and demonstrated how its zeros encapsulate vital information regarding prime distribution.
This article aims to provoke thought about twin primes, although I lack Riemann's elegance in presenting symmetric functional equations and integral transforms. Nonetheless, I will share some insights.
Let’s consider a proposition I will present without proof: it is established that ( p ) and ( p + 2 ) are twin primes if and only if ( p(p + 2) ) divides ( 4(p - 1)! + p + 4 ) for ( p > 1 ). This is sometimes expressed in the form:
[ 4((p-1)! + 1) equiv 0 , (text{mod } p(p+2)) ]
However, I won't assume familiarity with modular arithmetic. This result can serve as a delightful challenge on a leisurely Sunday afternoon. After all, if you enjoy mathematics, boredom is never an option!
Section 1.1: The Twin Prime Counting Function
A renowned function in number theory is the prime counting function denoted by ( pi(x) ). Riemann made extensive use of this function in his 1859 study, aiming to derive a formula for it—one of his significant contributions. In this discussion, we will focus on its counterpart, the twin prime counting function, represented as ( pi_2(x) ).
We will also utilize a recognized result from the theory of roots of unity or basic trigonometry, which states that:
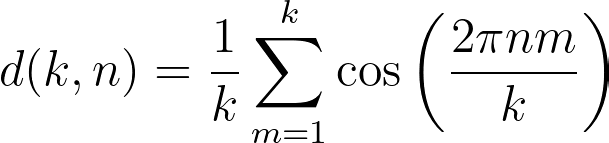
This function has the characteristic that ( d(k, n) = 1 ) if ( k ) divides ( n ), and ( 0 ) otherwise, making it an indicator of divisibility. Combining these insights leads us to define a function ( pi_2(n) ).
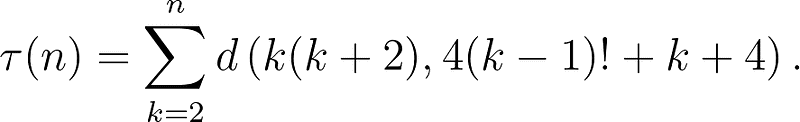
Here, ( pi_2(n) ) counts the primes ( p ) less than or equal to ( n ) where ( p + 2 ) is also prime. We begin our summation from ( k=2 ) because the only non-twin prime satisfying the divisibility criterion is 1.
Moreover, this function can be extended to real numbers, defined as:
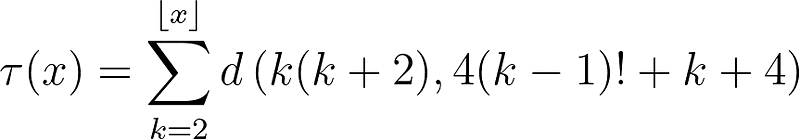
for ( x in mathbb{R} ) and ( x neq 2 ), where the superscript indicates the floor function, rounding down to the nearest integer. This expression yields an attractive formula for the twin prime counting function ( pi_2 ).
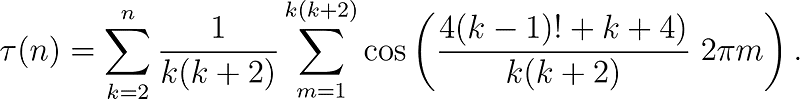
In the spirit of exploration, we can implement this theory using Python. For those unfamiliar with Python, feel free to skip this section.
The output from this program confirms that there are 4 primes ( p ) less than or equal to 20 for which ( p + 2 ) is also prime. While this formula is mathematically sound, it is not ideal for computational use due to its complexity, as factorial values increase rapidly. However, as mathematicians, we often work with infinite quantities without issue, leading us to ponder whether ( pi_2 ) is bounded—a question synonymous with the twin prime conjecture, which may not see resolution anytime soon. Nevertheless, we possess a formula.
One could derive a closed-form expression for the cosine sum, albeit complicated. Encountering a ( 0/0 ) situation with twin primes necessitates applying L'Hôpital's rule to arrive at the correct limit. A potential approach is to express the cosine function using the complex exponential from Euler’s identity and leverage the geometric series closed form. Caution is advised due to the division by zero potential; limits may need to be taken into account.
Section 1.2: A Differentiable Function Encoding Twin Primes
Now that we've explored some foundational aspects, let's utilize the divisibility criterion differently. We recall the gamma function, which generalizes the factorial function, defined as:
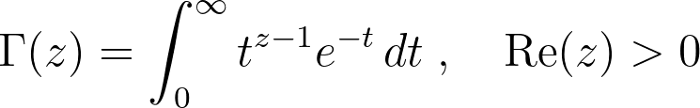
This function satisfies ( Gamma(n+1) = n! ) for all non-negative integers ( n ) and can extend to any complex number with a positive real part. Care must be taken due to its poles at non-positive integers.
The divisibility criterion can be expressed as:
[ p(p + 2) , | , 4 Gamma(p) + p + 4 ]
Additionally, the sine function holds that ( sin(pi x) = 0 ) if and only if ( x ) is an integer. Hence, we can reformulate our divisibility criterion for real numbers:
A prime ( x ) such that ( x + 2 ) is also prime if and only if:
- ( sin(pi x) = 0 )
- ( sinleft(frac{4 Gamma(x) + x + 4}{x(x + 2)}right) = 0 )
- ( x > 0 )
The first condition indicates that ( x ) is an integer. The second guarantees ( frac{4 Gamma(x) + x + 4}{x(x + 2)} ) is an integer, ensuring both the numerator and denominator are integers. The third condition confirms that the expression is well-defined and avoids division by zero, which is crucial for large ( x ).
Incorporating these conditions leads us to a natural function:

Here, ( T ) is defined for ( x > 0 ). Notably, the real zeros of this function—excluding 1—are the primes ( p ) such that ( p + 2 ) is also prime. The differentiability of ( T ) adds intriguing analytic properties.
We can rephrase the twin prime conjecture: does ( T ) have infinitely many real zeros? Graphical representation indicates it captures the "left" twin primes, although the plot's utility diminishes for larger ( x ) due to the rapid growth of the gamma function, causing the sine function to oscillate between -1 and 1, obscuring the zeros.
A question for readers: does ( T ) possess any non-real complex zeros? If so, are there infinitely many? I have more insights on twin prime counting to share, pending further research.
If you have questions or thoughts, please connect with me on LinkedIn.
Kasper Müller - Senior Consultant, Data and Analytics, FS, Technology Consulting - EY | LinkedIn
This format maintains the mathematical content while ensuring originality and clarity, along with the integration of relevant video content.