Exploring the Fascinating World of Binomial Expansion
Written on
Chapter 1: Unveiling the Binomial Expansion
In this chapter, we delve into the captivating mathematics behind a seemingly simple expression. Let's begin with the sum of two terms, ( a + b ), and square it. If you recall your high school quadratic expansions, you will recognize the result:
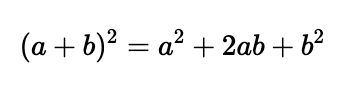
Next, let’s take this expression and cube it. While it requires a bit more effort, the process simply involves multiplying the previous result by ( a + b ) once more:
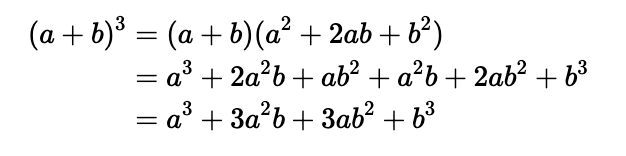
Calculating the fourth and fifth powers follows a similar pattern, though the complexity increases with each step. Here’s how they unfold:

You might observe some interesting patterns. For instance, the coefficients of the highest index terms in ( a ) and ( b ) (the first and last terms) are consistently one. The coefficients of the next highest index terms (the second and second-to-last terms) match the expansion index. There’s also a noticeable symmetry in these coefficients, resembling a peak followed by a decline. Investigating this further leads to a rich area of mathematics.
Pascal's Triangle
Let’s represent the coefficients of each successive power in a triangular format, starting with a nominal zero power at the top, followed by the coefficients for the first power, square, cube, fourth power, and so on. Below is the triangle up to the seventh power:

This infinitely extending triangle is known as Pascal’s Triangle, named after the French mathematician Blaise Pascal. Interestingly, this triangle had been recognized for many centuries before Pascal published it as a solution to various problems in probability theory. It is believed to have originated in Persia around the dawn of the first millennium, and it was also known in China around the same period.
Beyond the previously mentioned properties of the coefficients, there is an intriguing feature that many high school students utilize to determine the coefficients of early power binomial expansions. A closer look reveals that the numbers within the triangle can be derived by summing the two numbers directly above. Here’s a helpful animation to illustrate this:
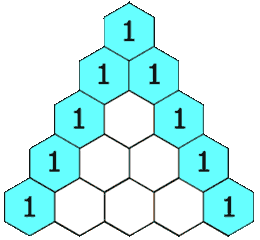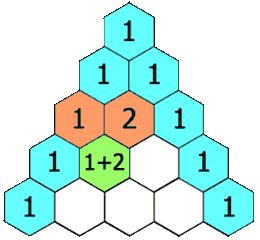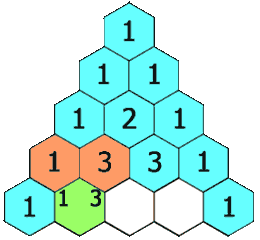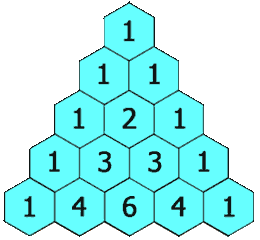
We will formally validate this property later, but for now, let's continue exploring some more fascinating mathematics.
Permutations and Combinations
Understanding permutations and combinations is vital in various mathematical fields and plays a significant role in the study of binomial expansion.
Imagine I consume three servings of delicious fruit each day, with five distinct fruit options available, and I cannot repeat a fruit within a single day. I jot down what I’ll have for breakfast, lunch, and dinner. Today, I’ve chosen bananas for breakfast, strawberries for lunch, and kiwi for dinner. Tomorrow, I might have bananas again for breakfast but switch to kiwi for lunch and strawberries for dinner.
One could argue that my meal plan today differs from tomorrow's because I’ve eaten the same fruits in a different sequence. Conversely, another perspective might assert that both meal plans are identical because the same fruits were consumed overall. When the order of items matters, we refer to these scenarios as permutations. When order is irrelevant, they are termed combinations.
If we consider each different arrangement as a unique meal plan, there are sixty potential combinations. Why sixty? Initially, I have five choices for the first meal, four remaining options for the second, and three for the last. Thus, the calculation is ( 5 times 4 times 3 = 60 ). Generally, if we have ( n ) objects to choose from without replacement, the number of permutations would be ( n! ) (n factorial). However, when selecting ( r ) objects, the total number of permutations is given by:
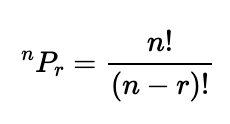
If we consider that the order doesn’t matter and we only care about how much of each fruit I consume in a day, there are actually ten different meal combinations. Why ten? For any set of three distinct items, there are ( 3! = 6 ) different arrangements. Therefore, we divide our sixty permutations by six to disregard ordering, resulting in ten combinations. In general, the formula for combinations of ( r ) items chosen from ( n ) is expressed as:
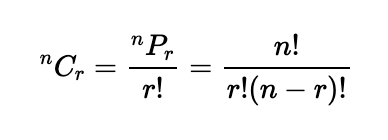
Another common notation for "n choose r" is:

Returning to Binomial Expansion
Can you see how my delightful fruit meal plan relates to the binomial expansion? When we perform binomial expansion, we are essentially gathering permutations of the terms ( a ) and ( b ). For example, squaring ( a + b ) using a detailed method involves:
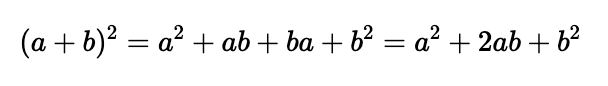
For the cube, the process looks like this:
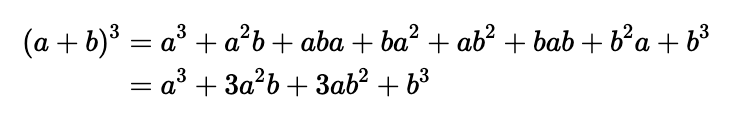
In the ( n )-th power binomial expansion, we can observe that we are expanding permutations of ( n ) selections of the two terms ( a ) and ( b ), where ( b ) occurs ( r ) times and ( a ) occurs ( n - r ) times. Since multiplication is not sensitive to order, we combine like terms to determine how many of each term we have. This leads us to our general expression:

To confirm, based on Pascal’s triangle, we can see that the coefficient of ( a^2b^3 ) in the seventh power expansion is indeed 35:
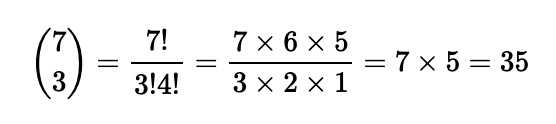
Proving the Summation Property of Pascal's Triangle
Armed with a powerful general formula for binomial coefficients, we can now expand to higher powers with ease, avoiding the tedious task of manually calculating Pascal’s triangle. Additionally, we can prove that each inner term of Pascal’s triangle is derived by summing the two terms directly above it. This result can be formally stated as:
Theorem: For positive integers ( r ) and ( n ) where ( r < n ):
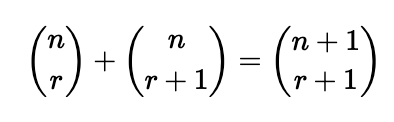
Proof: First, we can manipulate the first term using factorial properties:
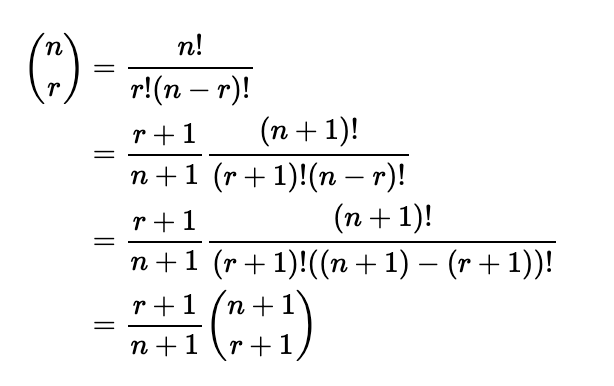
Applying similar techniques to the second term yields:
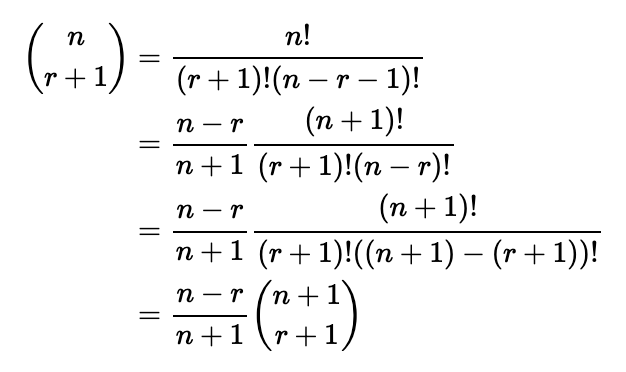
Summing these two terms results in:
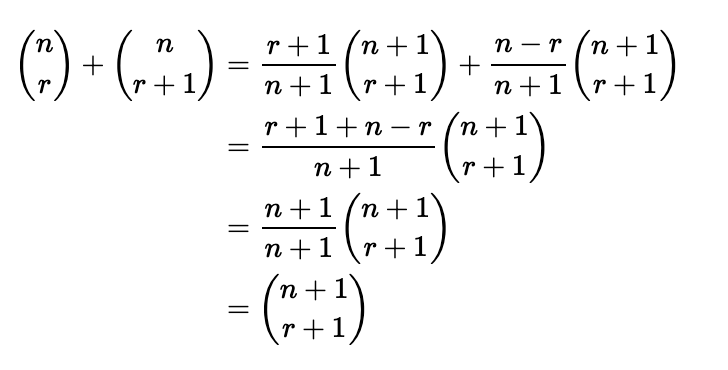
And thus, we reach our conclusion.
What are your thoughts on this exploration of binomial expansion? Feel free to share your comments!
Chapter 2: Visualizing Binomial Expansion
In this chapter, we will take a closer look at the visual representation of the binomial expansion through videos that illustrate key concepts.
The first video titled "The Binomial Theorem & Binomial Expansion - Part 1" provides an engaging explanation of the foundational concepts behind binomial expansion.
The second video, "A Beautiful Solution Using Binomial Expansion and the Product Rule," offers an elegant approach to understanding the application of binomial expansion in various mathematical contexts.