When I first learned that bacteria outnumber human cells by a factor of ten, it struck me as unsettling to think that I was primarily a vessel for microbial life. This morbid idea is compelling, and here's why.

The concept of bacteria vastly outnumbering human cells is fascinating because, like many, I picture bacteria as tiny, insignificant entities that only seem powerful when they cause disease. Realizing that humans are "mostly bacterial" transforms the perception of bacteria from weak to intriguing, as they are intrinsically part of us. As Ed Yong aptly put it, “I Contain Multitudes.”

However, this ten-to-one ratio is likely a misconception; current estimates suggest that bacteria and human cells coexist in roughly equal numbers. Nevertheless, I still view bacteria as formidable organisms condensed into minuscule forms.

Last year, my perspective on the microbial world deepened during a class at Caltech titled Physical Biology of the Cell, led by the enigmatic Rob Phillips. As a graduate student in his lab, I felt compelled to enroll.

Anticipating a semester filled with complex equations, I was surprised to find the initial weeks focused solely on arithmetic, specifically on what the syllabus termed order-of-magnitude thinking.

Order-of-magnitude thinking allows one to estimate values using little more than mental arithmetic, paper, and a pen. Imagine being stranded on a desert island where rescue hinges on answering questions like, “How many red blood cells are in a human body?” or “How many viruses are present in a drop of ocean water?” While exact answers elude us, we can approximate them effectively.

In this approach, any answer that falls within a factor of ten of the actual figure is deemed acceptable. Calculations rely on tens as multipliers, results are rounded, and educated guesses are essential. This technique offers a relaxed yet efficient form of algebra.

Why, then, did a course in physical biology—where researchers typically utilize highly sensitive instruments for precision—begin with such a casual approach?

I later realized that much of biology necessitates approximate solutions. Whenever scientists prepare growth media, dilute chemicals, or engage in similar tasks, they must first ascertain the quantities of materials involved. For instance, how much DNA can be extracted from 5 milliliters of E. coli? How much glucose is required to cultivate a liter of yeast? These inquiries demand order-of-magnitude reasoning.

Outside the laboratory, this basic level of estimation proves even more potent. By engaging in thoughtful contemplation, we can begin to quantify our surroundings. Many individuals lack an understanding of the relative sizes of entities, such as how minuscule a bacterium is compared to a human or how a human measures against a planet. Order-of-magnitude thinking helps contextualize our world.

During the pandemic, with ample free time, I found myself pondering whimsical biological questions and tackling them with order-of-magnitude reasoning. Some questions were peculiar, like, “How long would it take for bacteria to consume the Earth if they divided every 30 minutes?” Others were simply intriguing, such as, “How many bacteria would collectively weigh one gram?”

These questions will be addressed in this article. Remember, the process of arriving at an answer holds as much significance as the answer itself. I hope you enjoy the experience of thinking through and solving these problems with just your mind, paper, and a pen.

Before delving into the ambitious query of bacteria consuming the Earth, we must first establish a foundational understanding. Let's clarify the misconception of bacteria outnumbering human cells. A 2016 research article indicates that “the number of bacteria in the body is actually comparable to the number of human cells, with their total mass being approximately 0.2 kg.”

This suggests that the numbers of human and bacterial cells within our bodies are roughly equivalent. We can verify this claim: if a person harbors 0.2 kg of bacterial mass, how many cells are present?

To determine this, we first need to estimate the mass of a single bacterium. This task is challenging due to the diversity in bacterial shapes and sizes. Fortunately, we can use Escherichia coli as our “mathematical model.”

E. coli thrive in our intestines and can be observed under high-resolution microscopes. Typically, these cells measure 2 microns in length and 1 micron in width, resembling elongated, cylindrical blobs, with a volume of approximately 1 µm³. While this is an estimation, it suffices for our calculations.

A volume of 1 µm³ is minute, approximately 500 million times smaller than a grain of sand (assuming a grain has a diameter of 1 mm and a volume of 0.52 mm³).

Where do these figures originate?

When performing order-of-magnitude calculations, numerous resources can assist in verifying our estimates. The premier resource for biological values is BioNumbers, an online database compiling figures from thousands of peer-reviewed studies. For example, searching “protein size” yields relevant data, complete with units and the original research article. Each entry has a unique identifier (e.g., BNID: 113349), which I may reference throughout this article.

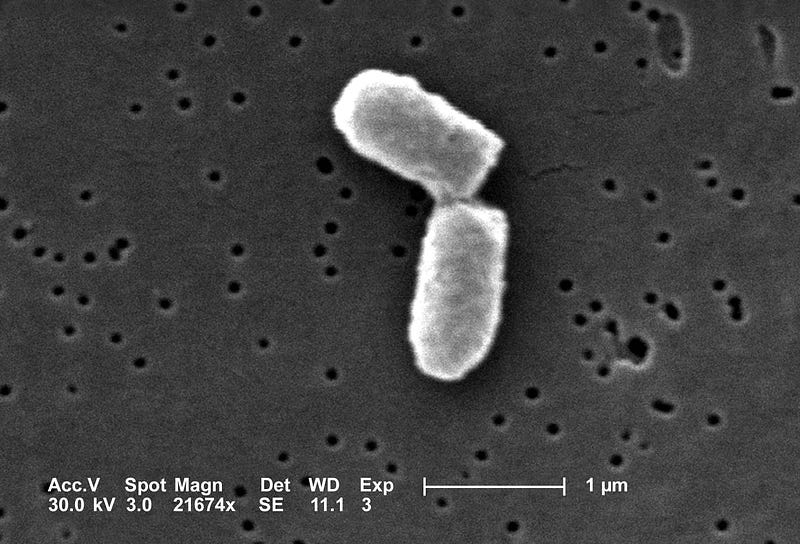
While a bacterial volume of 1 µm³ is indeed small, grasping just how small it is requires context and comparisons.

To illustrate, consider items smaller than a bacterium. Viruses are a prime example; a typical virus measures about 100 nanometers in diameter. If approximated as spheres, about 2,000 viruses can fit inside a single bacterium, and roughly 200,000 viruses could fit within a human cell, which is about 100 times larger than a bacterium. It takes approximately 1,000 viruses lined up side by side to span the width of a human hair.

Next, let's compare the size of a protein, the essential molecular machine that facilitates life processes. A typical protein measures about 5 nanometers in diameter (BNID: 100481) and has a volume of 65 nm³, meaning over 15 million proteins could fit into a single bacterium. Compared to viruses and proteins, bacterial cells are relatively large!

Returning to our initial question: how many bacterial cells reside in us if there is approximately 0.2 kg of bacterial cells within a 70 kg individual?

To resolve this, we first need to determine the mass of a single bacterium, a task complicated by their small size. Thankfully, we don’t need to weigh one directly; we can make an educated guess.

If we assume a bacterium has a volume of 1 µm³, we can estimate its mass based on reasonable assumptions. A common assumption for most organisms is that they are primarily composed of water.

Like most cells, bacteria consist of roughly two-thirds water. Consequently, if a bacterium has a volume of 1 µm³ and an approximate density of water (1000 kg/m³), its mass would be around 1 picogram. Given that there are 10¹² picograms in a gram, it follows that a trillion bacteria would collectively weigh just one gram.

With these foundational figures established, we can address more complex inquiries.

First, let’s revisit the question regarding the number of bacterial cells present in the human body. If the total mass of bacteria is 0.2 kg, dividing this by 1 picogram indicates there are around 2 x 10¹? bacterial cells within us.

This figure slightly exceeds the previously estimated value of 3.8 x 10¹³ from the research article, yet our estimate remains within an acceptable order of magnitude, which is the goal of these calculations. Now that we have a solid grasp of bacterial mass and volume, we can tackle larger-scale questions.

While size and mass are crucial metrics, they become even more engaging when we build upon these fundamental numbers to answer progressively intricate questions. The next question I wish to explore in this article pertains to a cell's metabolism. We’ll start with a straightforward inquiry and gradually increase the complexity.

Let’s investigate: “How many sugars are necessary to construct a cell?”

This question, along with its estimations, is derived from an insightful 2009 study published in the Proceedings of the National Academy of Sciences.

To arrive at an answer, we must make assumptions based on existing knowledge. For this inquiry, I will assume E. coli cells double approximately every 30 minutes—a fact I learned in research labs—and also assume these cells are roughly 70% water (BNID 100044). These seem like reasonable assumptions, and slight inaccuracies in our estimates are acceptable. The key is to thoroughly consider the problem and gain a deeper understanding in the process.

If a cell weighs 1 picogram and is about 70% water, it must consist of 30% cellular “stuff”—proteins, DNA, RNA, sugars, and various other chemicals. Assuming most of these compounds are denser than water, we can estimate that a bacterium's dry mass is around 0.5 picograms. This estimate is also supported by data (BNID 103892, 103904, 102230, 102242).

Let’s make one final assumption to refine our answer. We can posit that half of the 0.5 picograms of dry mass in a bacterium consists of carbon. This seems logical, as carbon is the fundamental building block of life and is present in all cellular components. Based on this assumption, a bacterium must contain approximately 0.25 picograms of carbon, equating to about 10¹? carbon atoms per cell (BNID 103010).

Since each glucose molecule comprises six carbon atoms, we can deduce that approximately 2 × 10? sugars are necessary to form a new cell.

Armed with this estimate, we can now address a thought-provoking question: “How long would it take for one bacterium to consume one sugar cube?”

In this hypothetical scenario, let's assume our tiny bacterial cell is joyfully consuming a sugar cube (the same kind you stir into your morning coffee) while producing a new cell every 30 minutes. Instead of remaining, this “daughter” cell washes away, while the parent continues to feast, creating clones indefinitely.

The question then becomes: how long would it take for that one cell, at peak metabolism, to devour the sugar cube?

Every 30 minutes, our hypothetical cell generates a clone, requiring 2 × 10? sugars for that process. To determine how many minutes it would take for our imaginary cell to consume the cube, we first need to calculate how many sugar molecules reside in a sugar cube.

A standard sugar cube weighs 4 grams (verified!), with a molecule of glucose weighing approximately 180 grams per mole, and containing 6.02 × 10²³ molecules per mole (known as Avogadro’s number). Performing the calculations reveals that a single sugar cube contains about 1.34 × 10²² glucose molecules. This number is roughly ten times more than the total number of stars in the universe or grains of sand on all the beaches on Earth. It’s an astounding quantity contained within a single sugar cube.

Dividing our estimate of 1.34 × 10²² glucose molecules in one sugar cube by the number of sugars required to sustain a cell every 30 minutes yields approximately 6.7 × 10¹². This indicates the fraction of glucose molecules in the sugar cube compared to those needed to construct a single bacterium. Multiplying this by the 30 minutes required to create a cell results in around 2 × 10¹? minutes before that one bacterium, at maximum metabolism, can consume a single sugar cube. This translates to about 382,420,091 years—remarkably, dinosaurs roamed the Earth roughly 240 million years ago.

Having completed these calculations, let's summarize the key values we've derived thus far:

1. A typical bacterium has a volume of 1 µm³ and weighs 1 picogram.
2. We assume that a cell divides approximately every 30 minutes.
3. It takes roughly 10¹? carbon atoms to build a cell.

Equipped with this quantitative foundation, we are now prepared to tackle the final question:

“How long would it take a growing colony of bacteria to consume the Earth?”

This is a complex inquiry, necessitating a gradual buildup of our understanding of bacterial metabolism and growth. The crux of this question lies in the term growing colony, indicating that we start with one bacterium and allow it to divide for days or weeks, provided with unlimited nutritional resources. If we continue to nourish the expanding colony, how long will it be before the Earth runs out of carbon-based materials?

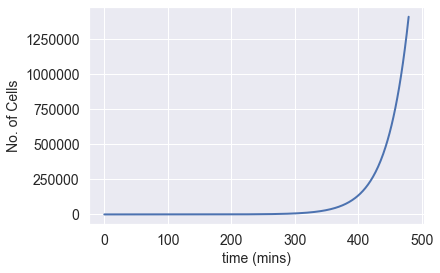
To begin, let’s estimate the rate at which bacterial cells divide. Using Python and Matplotlib, I created a line plot depicting the exponential growth of a bacterial colony (using numerical integration with the forward Euler method), assuming a division time of 33.3 minutes.

In just 8 hours, a single bacterial cell can generate over 1.5 million cells. If we let this colony thrive for several days (with unlimited nutrition), their population rapidly exceeds unimaginable figures. After a week, our hypothetical colony would reach over 10¹¹? cells—a number so staggering it defies comprehension. This is nearly one hundred orders of magnitude greater than the estimated number of stars in the universe (10²?).

In contrast, the known universe has a mass of only about 10?? grams. If each E. coli weighs one picogram, then 10?? E. coli would weigh as much as the entire known universe—a feat that could theoretically be achieved in just a few days.

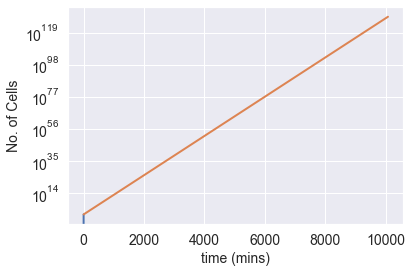
Fortunately, resources are not infinite; otherwise, the planet—and the universe—would soon be inundated with bacteria!

Understanding the rapid growth of a bacterial population does not answer our original question; to do so, we first need to estimate the total carbon available on Earth. A prior study titled “The biomass distribution on Earth,” published in PNAS, suggested that “the total biomass across all taxa on Earth is around 550 Gt C, with approximately 80% (around 450 Gt C) being plants.”

550 Gt is a substantial amount of carbon, but I suspect our theoretical bacterial colony would quickly deplete this supply.

To recall, a dividing bacterium requires about 10¹? carbon atoms to construct a single cell (BNID 103010). One gigaton is equivalent to one billion metric tons (10? tons). By converting 550 gigatons into actual carbon atoms using the molecular weight of carbon and Avogadro’s number, we can determine that the entire biomass of Earth is composed of roughly 2.75 × 10?? carbon atoms.

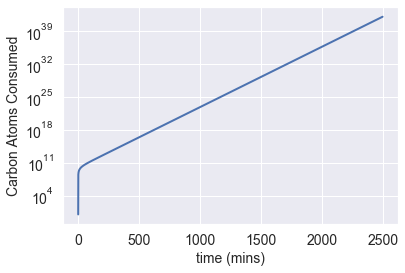
Using these estimates, I calculated the number of carbon atoms that our growing bacterial colony would consume after only 2500 minutes (nearly 42 hours). After less than two days, they would consume over 2.75 × 10?? carbon atoms.

In other words, it would take a bacterial colony, without nutritional limitations, less than two days to deplete the planet's carbon resources.

This result is remarkable, highlighting the true potential of exponential growth. Of course, this conclusion is based on estimates, and yes, we’ve made several assumptions (including that the colony can freely access all carbon stored in biomass).

However, this finding is significant as it illustrates just how limited Earth’s resources truly are. The idea that a colony of microscopic cells could potentially consume the planet's resources in two days, even theoretically, is a staggering thought.

Through these calculations, I aimed to demonstrate the efficacy and importance of order-of-magnitude thinking. This skill should not be confined to the prestigious halls of academia; everyone should be able to utilize basic algebra to make estimates that enhance their understanding both at home and in professional settings.

Many of the figures referenced in this article—such as the size, volume, and mass of a cell, along with the number of carbon atoms necessary for a bacterium—are sourced from the remarkable work of Rob Phillips, Ron Milo, and others.

Order-of-magnitude thinking serves as the initial framework for approaching a problem. Estimates provide insight into timing and scale, helping to contextualize various subjects. I find this way of thinking particularly relevant to biology, where comprehending the size and impact of organisms often eludes our understanding.

Now, go forth and start making your own estimates!